2024-11-28 東京大学
発表のポイント
- 細胞状態の制御可能性をベースに「細胞死」の数学的定義を提案、細胞数理モデルの生死を判定する数学的手法を開発した。
- 細胞死を数理科学として理論的に扱うことが可能になった。
- 「死」を定量的に理解するための基盤となる。
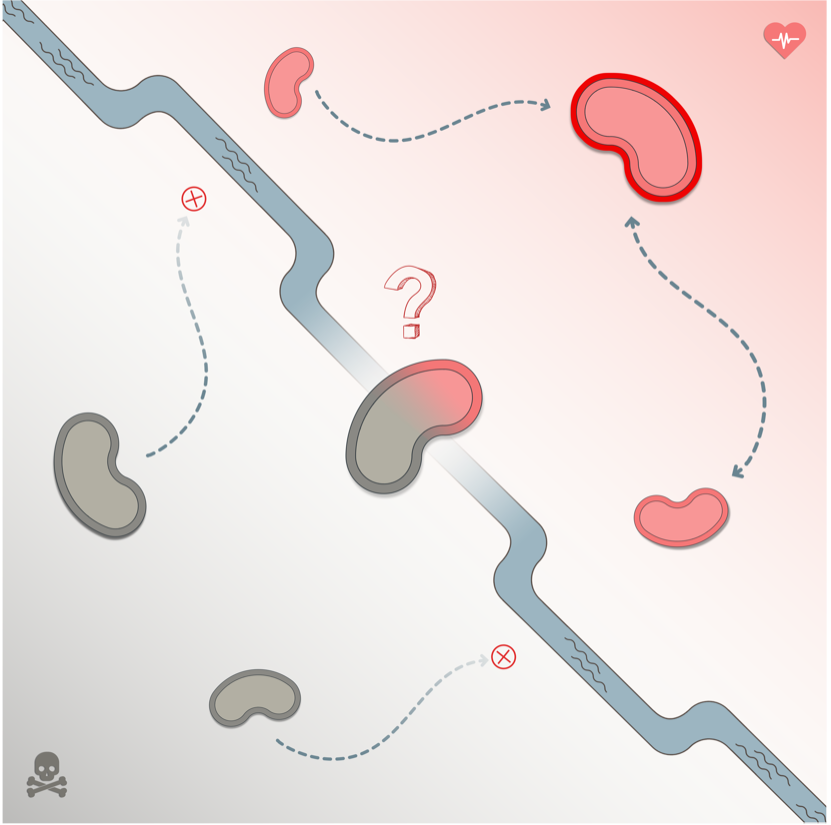
生きている状態と死んだ状態が制御可能性によって判定される(イラスト: 漆畑ドゥイチイヴァナ)
発表概要
今回、東京大学大学院理学系研究科の姫岡優介助教、大学院情報理工学系研究科 堀口修平大学院生(研究当時)と生産技術研究所 小林徹也教授からなるグループは、制御理論に基づいて細胞における「死」の数学的な定義を提案し、またこの定義のもと、代謝反応系の数理モデルが生きているのか、あるいは死んでいるのかを判定する手法を開発した。この手法を用いることで、細胞の「生きている」領域と「死んでいる」領域を、代謝物質の濃度空間などにおいて計算すること、すなわち「生命-非生命」を隔てる境界を計算することが可能となった。
本研究成果は、生きていることと死んでいることの本質的差異を抽出し、「生命とは何か」という生命科学の根本的な課題へと数理科学的にアプローチするための土壌となることが期待される。
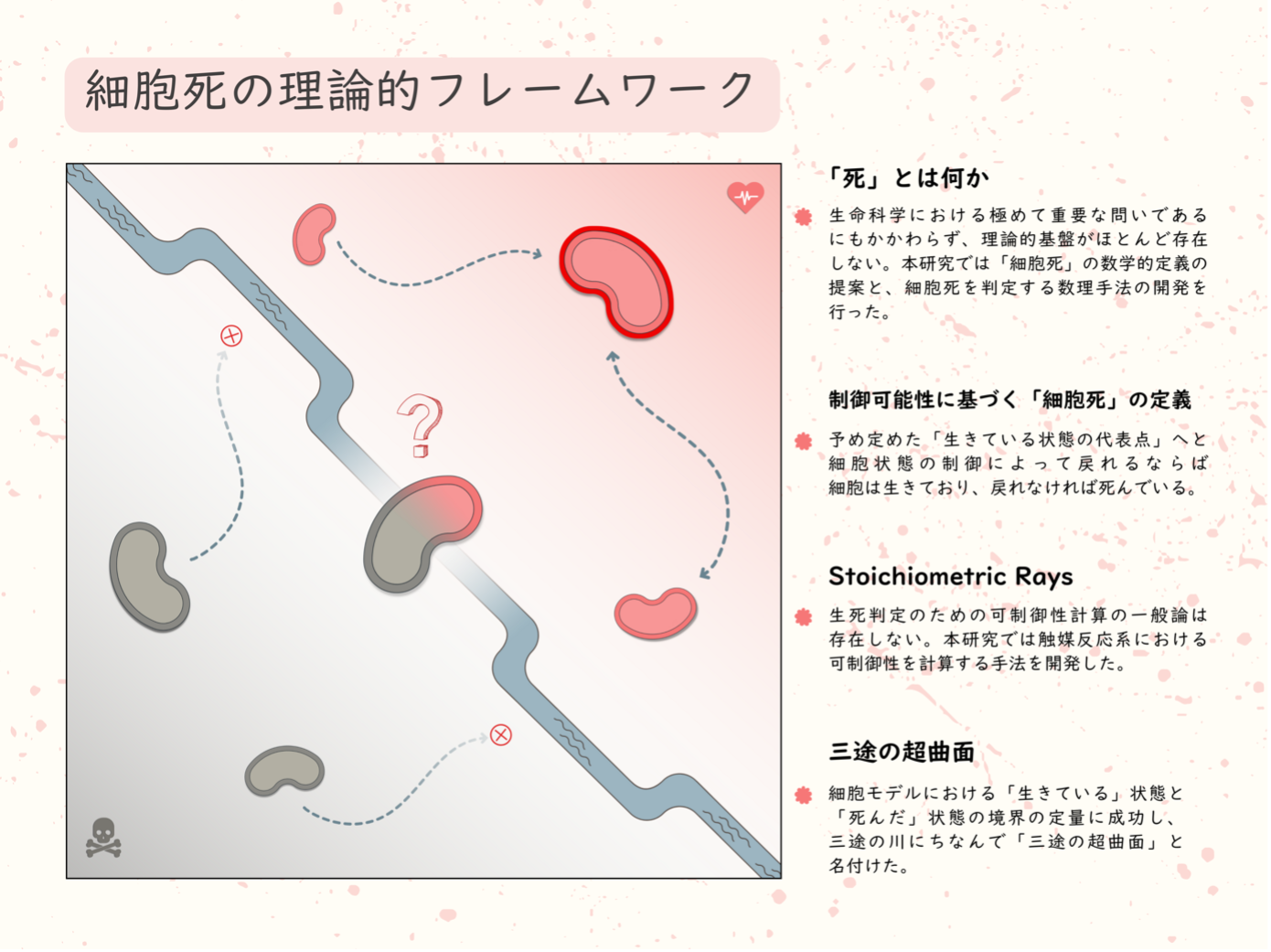
図1:本研究で提案した細胞死の理論的フレームワークの概略
あらかじめ定めた「『生きている状態』の代表点」(図右上で赤くハイライトされた細胞状態)へと制御によって復帰できるのであればその状態は生きており、そうでないならば死んでいる。生きている領域と死んだ領域を隔てるものがSeparating Alive and Non-life Zone (SANZ; 三途) 超曲面である。(イラスト: 漆畑ドゥイチイヴァナ)
発表内容
研究の背景
生命と非生命の違いとは何か—これは生命科学における根源的な問いのひとつである。「死」とは、「生命」が「非生命」へと転移する現象であるため、「死」を深く理解することができれば、生命と非生命の違いを明らかにすることができるかもしれない。そこで、細胞死を数理科学的に取り扱うための基盤の構築を目指した。なお、本研究では個体死と細胞死を区別する必要がない、微生物の死の理解を目標として想定している(注1)しかし本理論自体は微生物に限定されるものではなく、多細胞生物におけるアポトーシスといった、制御された細胞死についても適用することが可能である。
微生物学において、細胞死の実験研究は精力的に行われており、細胞死を判定するためのいくつかの実験的基準が存在する。頻繁に使用される手法には、細胞の生化学反応活性を測定するもの(MTT法、BONCAT法)、細胞の膜ダメージの度合いを定量するもの(PI染色法)、細胞の再増殖能力を測定するもの(プレーティングアッセイ)などがある。しかし、それぞれの手法は細胞の生命活性の異なる側面を定量しており、各手法からもたらされる生死判定が必ずしも一致しないことが問題となっている。
細胞死が実験的には精力的に研究されているにもかかわらず、細胞死に関する理論的研究はほとんどないと言っていい。「死」を数理科学的にどのように定義するべきか、また「死」という現象はどのような数理的性質を持つのかといった議論はほぼ手付かずの状態である。
研究内容
本研究では、「細胞状態や環境条件を制御することによって、あらかじめ定めた『生きている状態の代表点』(Representative Living State; RLS)へと戻れる状態は『生きている状態』であり、戻れない状態は『死んだ状態』である」という定義を提案した(図1)。この定義は、細胞の再増殖能力を計測するプレーティングアッセイの理論的な一般化に相当している。
また、本研究においては死の定義を提唱したのみではなく、上記定義に基づいた細胞代謝モデルの生死判定手法の構築にも成功した。上記定義において制御対象となり得るものには、外部栄養濃度や酵素濃度があるが、これらは物質量であるため負になることはできない。また、化学反応の速度を決定する反応レート方程式(注2) は通常、化学物質濃度の非線形な関数である。このような系の制御可能性は「制約付き大域非線形制御問題」と呼ばれる、極めて困難な問題クラスに属しており一般的解法は知られていない。しかし「触媒反応は平衡状態を変えない」という触媒反応における重要な法則に着目することで、触媒反応系において制約付き大域非線形制御可能性を計算するための数理手法、“Stoichiometric Rays”の開発に成功した。
本定義とStoichiometric Raysを用いた細胞モデルの生死判定を紹介する。ここでは簡単のために、4成分からなる単純な「おもちゃモデル」を用いることにする(図2A)。この代謝系には外部から物質Xが流入し、それがYへと変換され、系外へと排出される。多くの反応がATP、ADPというエネルギー通貨分子の変換反応と共役しており、XからYを作り、捨てることで正味1分子のATPを得ることができる。このおもちゃモデルは細胞の解糖系反応を単純化したものだと見ることもできる。図2Bには、酵素量などを一定値に固定した場合の反応系のダイナミクスを示した。系のダイナミクスは初期値に応じて、「活性状態」と呼んでいる状態(赤線)または「不活性状態」と呼んでいる状態へと収束する(青線)。活性状態ではXからYへと反応が流れ、ATP濃度が高く保たれている一方で、不活性状態ではXが途中で排出されてしまいATP濃度が低くなっている。つまり前者が正常な代謝状態、後者が異常な代謝状態である。
活性状態を『生きている状態の代表点』とした場合に、不活性状態は死んでいる状態と言えるのだろうか。それとも何らかの制御を行えば活性状態に戻ることができるのだろうか。このモデルはATPとADPの総量が一定の3変数モデルである。そのため物質の濃度で表した状態空間(注3)を3次元で描くことができる。赤点、青点がそれぞれ活性状態、不活性状態に対応する(図2C)。Stoichiometric Raysを用いた計算によって、どのように酵素濃度や外部栄養濃度を制御しても、不活性状態から活性状態へと戻ることは不可能であるということが分かった。つまり不活性状態は『死んだ状態』である。さらに、図2Cにグレーで示した境界面をモデルの状態が横切ると、二度と活性状態へと戻れなくなることも明らかになった。この境界面は、渡ってしまえば二度と『生きている状態』に戻れない、三途の川に相当するものであると考えることができる。我々はこの境界面を三途の川になぞらえてSeparating Alive and Non-life Zone (SANZ) 曲面と名付けた。
本研究を実験・理論の両面からより発展させることで、「死」を定量的に深く理解し、またその制御を可能とするような学理の展開が期待される。
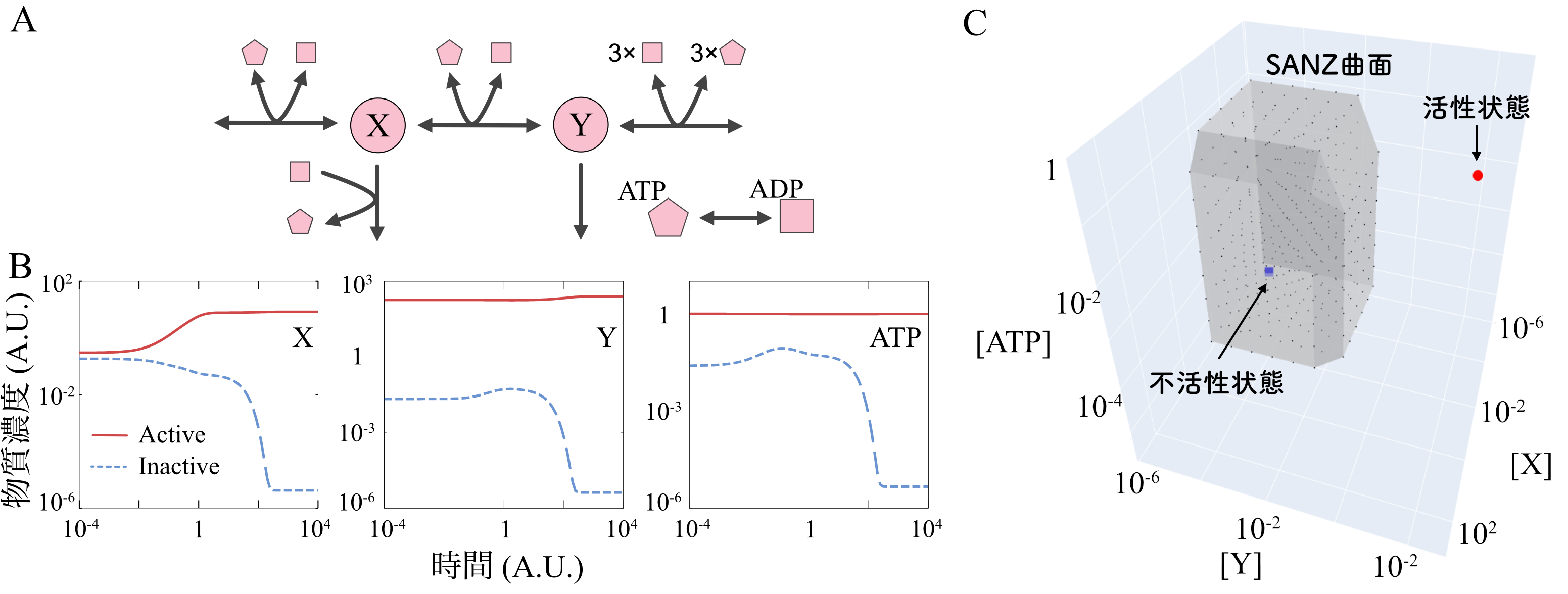
図2:細胞代謝のおもちゃモデルにおける生死境界の計算
(A) 細胞代謝のおもちゃモデル。Xを取り込み、Yを排出する過程で差し引き1分子のATPを得ることができる。(B)異なる状態を初期値として選んだ場合、モデルは2ß通りの定常状態へと緩和する。(C)X, Y, ATPの濃度を用いて描いた状態空間。赤点と青点がそれぞれ活性状態、低活性状態である。グレーの境界面(SANZ曲面)を跨ぐと二度と活性状態へと復帰することが不可能になり、不活性状態に落ちていくしかなくなる。不活性状態はSANZ曲面に囲まれた領域の内側にあることに注意
論文情報
- 雑誌名
Physical Review Research論文タイトル
Theoretical basis for cell deaths著者
Yusuke Himeoka*, Shuhei A. Horiguchi, Tetsuya J. Kobayashi(*責任著者)
研究助成
本研究は、日本学術振興会 科学研究費助成事業(課題番号:JP22K15069, JP24K00542, JP19H05799)、学術変革領域(A)超越分子システム(課題番号:22H05403, 24H01118)、JST GteXバイオものづくり(課題番号:JPMJGX23B4)、JST CREST (課題番号:JPMJCR2011, JPMJCR1927) 日本学術振興会 特別研究員奨励費(課題番号:JP21J21415)の支援により実施されました。
用語解説
注1
「死」には「個体死」と「細胞死」が存在する。個体死とは、その生物個体を構成する個々の細胞がたとえ生きていたとしても、生物個体が生命機能を果たさなくなる現象である。日本において人間の個体死は「心拍動の停止」「自発呼吸の停止」「対光反射の消失・瞳孔散大」の3条件で判定される。細胞死は文字通り、細胞が死ぬことである。単細胞生物においては個体死と細胞死は同じであるため、分けて議論されることはない。本研究では細胞死に着目している。
注2
化学物質の濃度の関数として、化学反応の速度を与える関係式のことを反応レート方程式と呼ぶ。例えば物質Aが一定速度で物質Bになる不可逆反応の場合にその速度Jは、kを定数、[A]を物質Aの濃度としてJ = k[A]といった形で与えられる。多数の物質が絡む反応になると、より複雑な非線形の式になる。
注3
力学系理論において、モデルの変数を軸として構成した空間を状態空間と呼ぶ。例えば、2変数の化学反応モデルであれば、物質1の濃度をX軸、物質2の濃度をY軸にとった2次元平面が状態空間となる。状態空間の一点一点がモデルの各状態に対応するため、状態空間を用いるとモデルが取りうる状態を鳥瞰することができる。