2024-04-25 理化学研究所
理化学研究所(理研)脳神経科学研究センター 数理脳科学研究チームの寺田 裕 基礎科学特別研究員(研究当時)と豊泉 太郎 チームリーダーの研究チームは、神経ダイナミクスのカオス[1]を用いて、環境状態の推定を行う脳型のベイズ計算[2]機構を提案しました。本研究成果は、脳の情報処理メカニズムの原理の解明、特に神経活動のダイナミクスを用いた推論の理解に貢献すると考えられます。また、脳を模倣したニューロモルフィック計算機[3]など人工知能や機械学習への応用も期待されます。
今回、研究チームは、神経細胞間の情報伝達を担うシナプス結合[4]の効果で生じる神経活動のカオスに着目しました。提案した脳の神経回路[5]のモデルでは、感覚入力がたとえ一定であっても、シナプス結合による神経細胞間の相互作用を使って時間とともに揺らぐ神経活動を積極的に生成します。このように生成された神経活動は微小な変動による誤差が将来の大きな誤差に拡大する性質を持つためカオスと呼ばれます。従来の研究では、カオスは情報処理にとって不利益であると解釈されていましたが、本研究ではカオスを利用してベイズ計算を行う脳型モデルを提案しました。本モデルは、ベイズ推定の事後分布から予測される多様な事象を表現するために、カオスによって生じる神経活動の動的な揺らぎを活用する統計サンプリング手法を使用しています。本研究結果は、脳がカオスによる揺らぎを利用して機械学習の生成モデル[6]に類似した確率的サンプリングを行う場合にどのような計算論的利点が予想されるかを示しています。
本研究は、科学雑誌『Proceedings of the National Academy of Sciences(PNAS)』オンライン版(4月22日付)に掲載されました。
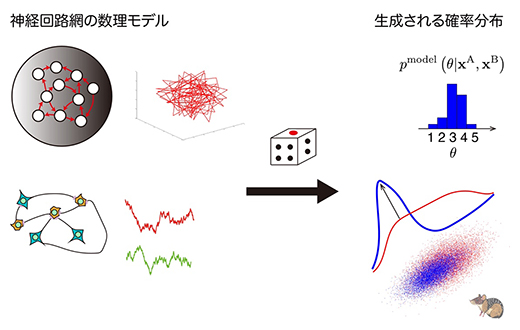
カオス的な神経活動を利用して確率的推論を行う神経回路の数理モデル
背景
脳は不確実な情報を処理する必要があります。例えば、猟を行う状況で動物は獲物の位置を特定しなくてはなりません。このとき目や耳などからの感覚入力を得て獲物の位置を推定しますが、得られる感覚情報はしばしば不完全であり、位置を完全に特定することはできません。そのため、それぞれの感覚情報の信頼性を評価し、複数の感覚情報を統合して「獲物の位置に関する確率分布」を計算しなければならない状況が生じます。このような設定において、数理的に最適な推定方法としてベイズ推定があります。これまでの神経科学の研究から、動物や人間は不確実性のある状況下で、最適に近い推定をしていることが報告されています。しかし、脳がどのようにその計算を実装しているのかはよく分かっていませんでした。
他方、脳の神経活動を観測した実験から、神経細胞はたとえ感覚入力が一定もしくは入ってこない状況でも常に動的に揺らいでいることが観測されています注1)。しかし神経活動の揺らぎがどのような機構で生成されているかはまだ十分に分かっていません。別の研究で、感覚入力がない状況の脳の神経活動がベイズ推定に用いる経験的事前分布[7]に対応していると解釈できることを報告している注2)ものもありますが、その仕組みは分かっていませんでした。
神経活動の揺らぎの生成機構に関する仮説の一つとして、非線形なダイナミクスを持つ神経細胞の活動がシナプス結合によって相互作用することでカオスに発展し、その結果、感覚入力が一定でも神経活動が揺らぐようになるのでないかという提案があります。しかし、このようにして生じる神経活動のカオスダイナミクスは不規則であり、またバタフライ効果によって微小な変動の効果も時間とともに拡大していく鋭敏さを持つため、脳の情報処理に有益な役割を果たすかどうかは分かっていませんでした。
注1)Tomko, G. J. & Crapper, D. R., “Neuronal variability: non-stationary responses to identical visual stimuli.” Brain Res. 79, 405-418 (1974).
注2)Berkes, P., Orbán, G., Lengyel, M., & Fiser, J., “Spontaneous cortical activity reveals hallmarks of an optimal internal model of the environment.” Science, 331, 83-87 (2011).
研究手法と成果
動物が獲物を捕える際に、脳が獲物の位置を複数の感覚情報に基づき推定する問題を考えます(図1)。
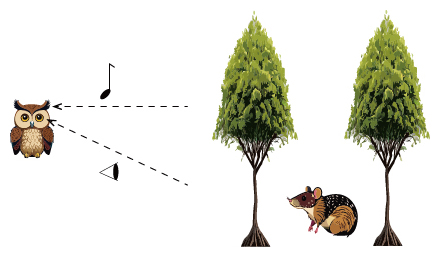
図1 手がかり統合タスクの例
例えば、フクロウがネズミを捕獲するためにネズミの位置を推論する状況を考える。この推論を解くためには目から得られる視覚情報と耳から得られる聴覚情報といった複数の感覚入力からの情報を適切に統合する必要がある。本研究ではこのタイプのタスクを考え、それを神経回路の数理モデルに学習させた。このとき、感覚入力によって得られる情報は不確実性を含み、必ずしも推定される位置が一つに定まらない。例えば、暗い環境では視覚情報の不確実性が大きく、聴覚情報とうまく組み合わせることで、獲物の位置に関する確率分布の推定を適切に行うことができる。
この問題は、数理的に、感覚情報の統合を要するベイズ推定の問題として定式化することができます。今回、この問題を解くために、揺らぎを生成し利用するリカレントニューラルネットワーク[5]の学習機構を提案しました(図2)。機械学習の分野においては、このようなリカレントニューラルネットワークの学習に誤差逆伝搬法[8]をよく用います。しかし、誤差逆伝搬法を実装するためには、シナプスの信号伝達とは逆向きに異なる種類の信号(誤差信号)を伝搬する必要があり、その際、順方向と逆方向のシナプス伝達効率が一致していなければなりません。このような要請から、生物学的に誤差逆伝搬法を実装するのは困難だと議論されています。そこで本研究では、より生物学的に妥当だと考えられている摂動法[9]を用いてリカレントニューラルネットワークを学習するというコンピュータシミュレーションを行いました。
学習の結果、感覚入力が一定であっても、リカレントニューラルネットワークの神経活動ダイナミクスはカオスによる揺らぎを生成するようになり、複数の感覚入力を統合して得られるベイズの事後確率分布に従って、起こり得る事象(獲物の位置)のサンプルを生成し表現するようになりました(図2)。
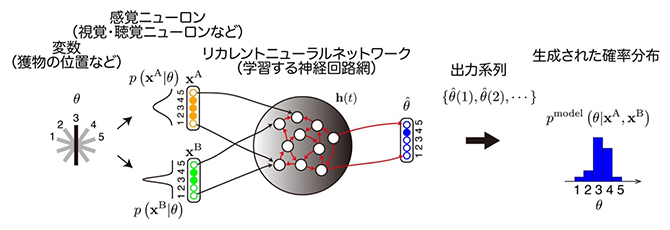
図2 手がかり統合タスクに対するリカレントニューラルネットワークを用いた定式化
変数θの値が定まると、感覚ニューロンがそれに応じて発火活動パターンを確率的に決める。リカレントニューラルネットワークはこの感覚ニューロンの発火パターンから背後にある変数の値に関する確率分布を計算する。ネットワークのダイナミクスによって生成される各時刻の活動パターンを確率事象のサンプリングと見なすことで、確率分布を表現する。学習後はこのようにして計算した確率分布が変数θに関する事後分布を表現する。
このような学習の後には、たとえ感覚入力のない状態でもリカレントニューラルネットワークはカオスによって自発的に揺らぎを生成するようになりました。そこで、研究チームが一部もしくは全部の感覚入力が与えられない状況でネットワークが生成しているサンプル事象の分布を解析したところ、その状況で推論する際に理想的な確率分布(観測されない感覚入力の影響について事後分布を平均した後の確率分布)を表現していることが分かりました(図3)。この性質は、感覚入力がない場合に脳活動が経験的な事前分布を表現しているという実験的な知見とも合致しており、リカレントニューラルネットワークが全ての感覚入力が与えられた状況の学習結果を、感覚入力がない状況にもよく汎化[10]できたことを示しています。
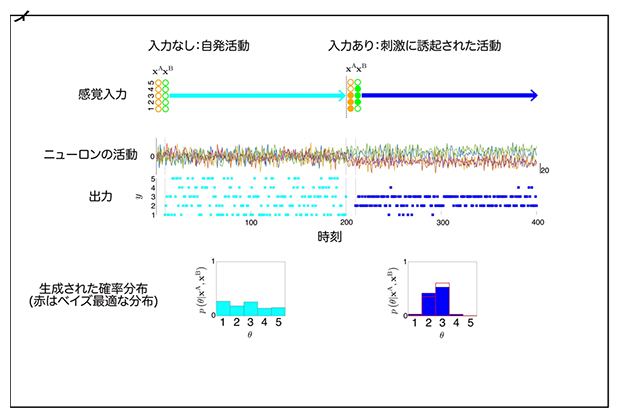
図3 神経ダイナミクスによる事後分布からのサンプリング
学習されたリカレントニューラルネットワークはカオス的な神経活動を用いて生成したサンプリングによって事後分布の表現を行う。感覚入力がある場合は、その入力を基にした事後分布からサンプリングを行う。感覚入力がない場合は、リカレントニューラルネットワークは自発活動を示すが、その活動は事前分布を表現している。
この他、研究チームは同様の方法で表現すべき事象(獲物の位置など)が動的に変化する問題も解くことができることを示しました。実生活において環境は時間とともに遷移していくため、その遷移確率を学習できる脳型モデルは、生物の情報処理メカニズムを理解する上で重要な知見を与えると考えられます。
以上のように、研究チームは、神経回路の数理モデルであるリカレントニューラルネットワークを用いた生物学的学習法を提案しました。学習後、ネットワークは複数の感覚入力を統合し、カオスを利用したサンプリングによって環境変数の事後分布を表現するようになり、一部の感覚入力がない状況でも学習結果を汎化するようになりました。このことは、脳がカオスによる揺らぎを用いた生成機械である可能性を示唆しています。
今後の期待
本研究成果は、脳神経系の神経活動ダイナミクスと情報処理との関係を理解する上で重要な示唆を与えています。既存研究において、カオスはしばしば情報処理の信頼性を低下させる避けるべき性質と捉えられてきました。本研究成果はカオスによる揺らぎの計算に対する役割を考える上での新たな視点をもたらしています。
また、本研究成果は脳の神経回路を模したリカレントニューラルネットワークによって、多様な感覚入力を統合し確率計算を行う方法を提案しており、ここでの揺らぎの活用方法は機械学習や人工知能分野の生成モデルに新たな知見を与える可能性があります。本研究で扱った学習方法は、エネルギー効率が高く分散型の情報処理を行う脳の働きから着想されたものであり、ニューロモーフィック計算機への親和性も高く、次世代情報処理計算機・アルゴリズム開発に向けた高い応用性が期待できます。
補足説明
1.カオス
動的な系を表す数理モデルのダイナミクスにおいて、摂動に対して大きな応答を示す状態のこと。1匹の蝶の羽ばたきが数日先の嵐を引き起こす例えからバタフライ効果と呼ばれる性質を持つ。
2.ベイズ計算
ベイズ推定とは、不確かな情報を基に物事の真の状態を推測する場合に用いられる統計的に最適な手法である。事前に持っている信念(事前分布)に、観測によって新たに得られた情報(視覚入力・聴覚入力など)を加えて、事後分布として推定したい変数(獲物の位置など)の取り得る確率を表現する。複数の観測によって得られた情報を統合することで、より確度の高い推定が可能になる。ここではベイズ推定を実装する際にニューラルネットワークが行う計算のことをベイズ計算と呼ぶ。
3.ニューロモルフィック計算機
神経回路網の性質から発想を得て開発されている計算機。高いエネルギー効率や分散情報処理といった従来の計算機にない性能が期待されている。
4.シナプス結合
脳のニューロン間の接合部位のこと。一つのニューロンが放出する神経伝達物質が、次のニューロンの受容体に結合することで信号を伝える。シナプス結合が担うニューロンの相互作用によって、脳は複雑な機能を実現している。単体のニューロンの振る舞いが単純な場合でも相互作用することで複雑な神経活動のダイナミクスが生じる。
5.神経回路、リカレントニューラルネットワーク
複数のニューロンが互いにつながり、特定の機能を果たすためのネットワークのこと。神経回路は脳の情報を処理し、反応を生成する。感覚から思考、動作に至るまで、私たちの行動や認識の基盤となっている。このような神経回路のモデルとしてリカレントニューラルネットワークがある。リカレントニューラルネットワークとは、脳で観測されるようなループ構造(あるニューロンの出力が巡り巡って一部そのニューロンの入力として帰ってくる構造)を持つニューラルネットワークである。
6.生成モデル
トレーニングデータを基に、データの生成方法を学習する人工知能モデルの一つ。このモデルは、トレーニングデータに類似した新しいデータを作り出すことができる。例えば、写真データから新しい画像を生成したり、テキストデータから新しい文章を作り出したりすることが可能。
7.経験的事前分布
これまでの経験によって構成される事前分布(上記[2]参照)のこと。例えば、動物が直近の感覚情報を受け取る以前に、過去の観測を手がかりに構成する事前分布のこと。
8.誤差逆伝搬法
ニューラルネットワークの学習アルゴリズムの一種。誤差関数の勾配を評価する際に、誤差信号をニューラルネットワークの出力側から入力側へと逆向きに伝搬することで計算する。
9.摂動法
神経活動やシナプス結合の強度に対する摂動を用いてシナプス結合の強度を更新する学習則。摂動を与えた結果、誤差関数がどのように変化するかを基に学習を行う。多様な摂動を与える必要があるが、簡易な機構で計算ができる。適切な条件の下では得られる勾配が誤差逆伝搬法によるものと一致することが示されている。
10.汎化
学習によって得られた結果を、学習の際に用いていないデータに対して一般化すること。一を聞いて十を知ったらうまく汎化できたことになる。
研究支援
本研究は、理化学研究所基礎科学特別研究員制度、科学技術振興機構(JST)戦略的創造研究推進事業(CREST)データ駆動・AI駆動を中心としたデジタルトランスフォーメーションによる生命科学研究の革新(研究総括:岡田康志)「多階層の神経活動データ駆動による睡眠脳の機能解明(研究代表者:井ノ口馨)」、日本医療研究開発機構(AMED)「革新的技術による脳機能ネットワークの全容解明プロジェクト」、日本学術振興会(JSPS)科学研究費助成事業新学術領域研究(研究領域提案型)「マルチスケール精神病態の構成的理解(領域代表者:林(高木)朗子)」、同若手研究「脳神経系が行う時空間情報処理に関する理論研究(研究代表者:寺田裕)」、米国エネルギー省Collaborative Research in Computational Neuroscience(研究代表者:Johnatan Aljadeff)による助成を受けて行われました。
原論文情報
Yu Terada, Taro Toyoizumi, “Chaotic neural dynamics facilitate probabilistic computations through sampling.”, The Proceedings of the National Academy of Sciences, 10.1073/pnas.2312992121
発表者
理化学研究所
脳神経科学研究センター 数理脳科学研究チーム
チームリーダー 豊泉 太郎(トヨイズミ・タロウ)
基礎科学特別研究員(研究当時)寺田 裕(テラダ・ユウ)
報道担当
理化学研究所 広報室 報道担当