2022-11-30 バッファロー大学(UB)
この論文は、神経細胞複合体の多次元的な形状によって単純なカスケードが編成されている。この論文では、ニューロンネットワークの数学的モデリングに関する新しい手法について論じている。
この研究の主な目的は、記憶をニューロンの活動パターンとして保存し、後で認知処理に確実に利用できるようにする生物学的・数学的メカニズムをよりよく理解することである。
神経細胞(電気信号によって脳や神経系全体に情報を伝達する細胞)をモデル化する過程では、神経細胞の生物物理学的および幾何学的特性を、グラフなどの数学的構造で表現することになる。
神経細胞ネットワークは、一連の入力(別の神経細胞に影響を与える神経細胞の活動)を神経細胞の反応に変換する非線形関数を用いて、記憶を符号化すると考えられている。
研究者たちは、これらのグラフを、ニューロンの広大なネットワーク間の接続をマッピングできる単純化された複合体、またはハイパーグラフに拡張することを提案している。
<関連情報>
- https://www.buffalo.edu/news/releases/2022/11/021.html
- https://www.nature.com/articles/s42005-022-01062-3
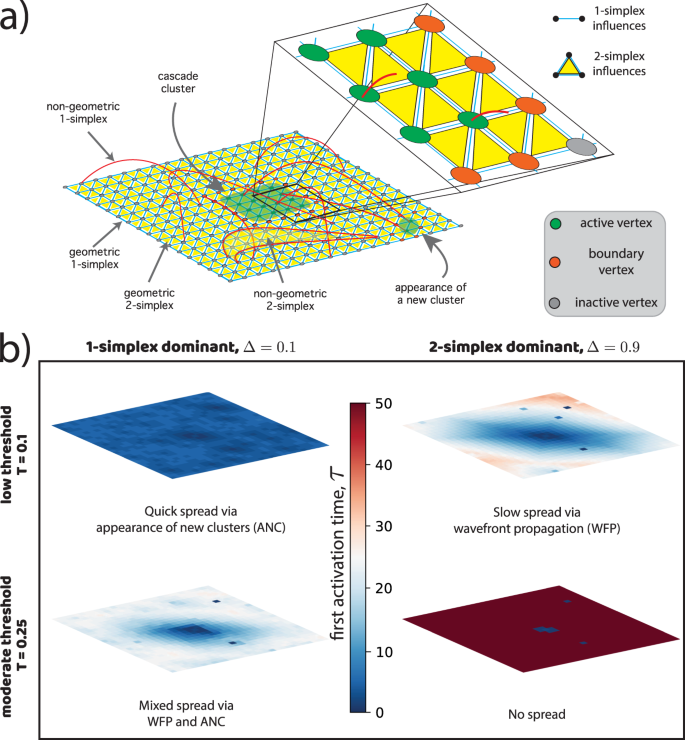
単純なカスケードは、神経細胞複合体の多次元的な幾何学的構造によって編成される Simplicial cascades are orchestrated by the multidimensional geometry of neuronal complexes
Bengier Ülgen Kilic & Dane Taylor
Communications Physics Published:08 November 2022
DOI:https://doi.org/10.1038/s42005-022-01062-3
Abstract
Cascades over networks (e.g., neuronal avalanches, social contagions, and system failures) often involve higher-order dependencies, yet theory development has largely focused on pairwise-interaction models. Here, we develop a ‘simplicial threshold model’ (STM) for cascades over simplicial complexes that encode dyadic, triadic and higher-order interactions. Focusing on small-world models containing both short- and long-range k-simplices, we explore spatio-temporal patterns that manifest as a frustration between local and nonlocal propagations. We show that higher-order interactions and nonlinear thresholding coordinate to robustly guide cascades along a k-dimensional generalization of paths that we call ‘geometrical channels’. We also find this coordination to enhance the diversity and efficiency of cascades over a simplicial-complex model for a neuronal network, or ‘neuronal complex’. We support these findings with bifurcation theory and data-driven approaches based on latent geometry. Our findings provide fruitful directions for uncovering the multiscale, multidimensional mechanisms that orchestrate the spatio-temporal patterns of nonlinear cascades.