シナプス遅延の漸近分布の存在を理論的に示唆～”最大値”の統計学を用いて神経伝達の遅延を探る～

2024-07-08

2024-07-06 東京大学

発表のポイント

神経伝達のシナプス遅延において、遅延の最大値に漸近分布が存在することを極値理論に基づいて新たに提唱し、この仮説の妥当性を数値シミュレーションによって示しました。
シナプス遅延の最大遅延の程度や頻度を定量的に評価する新しい統計指標を提供します。
将来において、神経ネットワーク全体の記憶や学習の上限(限界)の理論的な推定に役立てることが期待されます。

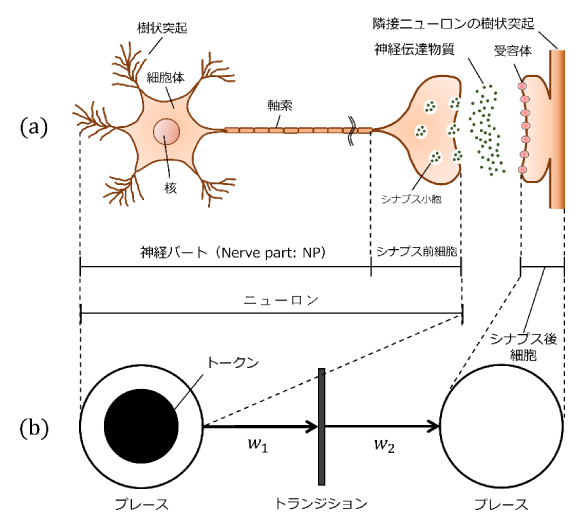
図1:単一ニューロンの状態遷移図(ペトリネット)を用いた記述
(a)は単一ニューロンの模式図、(b)はペトリネットで記述された2状態遷移モデルを示している。(b)の左側の白丸は(a)におけるNPとシナプス前細胞からなるニューロンの一部に対応し、(b)の右側の白丸は(a)におけるシナプス後細胞に対応する。スパイク信号はシナプス前細胞からシナプス後細胞へと一方向に流れる。(a)と(b)を比較すると、ニューロン間の伝達は2状態の遷移問題として記述できることが理解できる。

発表概要

東京大学先端科学技術研究センターの都築怜理講師の研究グループは、神経伝達のシナプス遅延(注1)において、遅延の最大値の漸近分布が存在することを極値理論(注2)に基づいて新たに提唱し、この仮説の妥当性を数値シミュレーションにより示しました。シナプス遅延がヒトの記憶や学習と密接に関連することは以前から知られていましたが、シナプス遅延の最大値やその発生頻度がどの程度かということについて、統計理論に基づいて定量的に予測する取り組みはこれまで行われていませんでした。本研究の成果により、神経伝達の最大遅延の程度と頻度を定量的に評価する新しい統計指標が提供されます。また、将来において神経ネットワーク全体の記憶や学習の上限(限界)の理論的な推定に役立てることが期待されます。

-研究者からのひとこと-

「神経ネットワーク」×「極値理論」のかけ合わせという、近い将来においてヒトの記憶と学習の上限(限界)を推定し、疾病における神経ネットワークの平常状態からの乖離の程度を評価するのに役立つことが期待できる新しい指標を提案しました。今後、AIや高性能シミュレーションと組み合わせて活用することで、より複雑な神経ネットワークへの応用が期待されます。(都築怜理講師)

発表内容

ヒトの脳内では約1000億個近くの神経細胞(ニューロン)が樹状突起を介して接続され複雑かつ巨大な神経ネットワークを形成しています。図1上段の図において、ニューロンの樹状突起で受信されたスパイク信号は軸索からシナプス前細胞に伝わり、シナプス前細胞から神経伝達物質がシナプス後細胞に伝達され、イオンチャネルを介して電気信号へと再び変換されて隣接ニューロンに伝達されます。このような神経伝達全体のメカニズムはResistor–Capacitor(RC)並列回路として記述できることが知られており、単一ニューロンの伝達プロセスに関する詳細な数理モデルとしては、イカの活動電位を測定した実験結果に基づいて1952年にHodgkin博士とHuxley博士によって提案されたHodgkin–Huxley Model(HHM)、活動電位(スパイク)の詳細な反応プロセスは考慮せずに膜電位の変位にのみ注目することでHHMにおける変数を減らして簡略化したLeaky Integrate-and-Fire Model(LIFM)などが有名です。

一方、これらの微分方程式による記述とは対照的に、スパイク信号の伝達は図1下段に示すように軸索とシナプス前細胞を合わせた部分とシナプス後細胞との間の状態遷移の問題とみなすことができます。シナプス後細胞にスパイク信号が到達する時刻の間隔は、神経伝達プロセスが微小粒子の物質輸送や生理化学反応に依存することから統計的に揺らぎます。したがって神経伝達プロセスは確率過程で記述でき、第一次近似的にはポアソン過程(注3)で記述できる問題だといえます。このときシナプスではスパイク信号の伝達に必要な生理化学反応や構造変化が原因となり、神経軸索の興奮伝導と比べて伝達に時間を要する現象(シナプス遅延)を生じます。シナプス遅延がヒトの記憶や学習と密接に関連することは以前から指摘されていましたが、遅延の最大値やその発生頻度がどの程度かということについて、統計理論に基づいて定量的に予測する取り組みはこれまで行われていませんでした。

本研究では、(1)スパイク信号の伝達がポアソン過程で記述できること、および(2)シナプス遅延のヒストグラムが指数分布(またはパレート分布)に従うことを示す先行研究(Wierenga CJ et al., 1999 等)の事実に基づいて、シナプス遅延における最大遅延の頻度分布(またはその確率密度分布)には漸近分布が存在し、それは極値理論(Extreme Value Theory: EVT)における極値分布に等しいという仮説を立てました(極値分布については図2下段を参照)。なぜならばEVTでは、ある確率変数列が指数分布に従う場合、その最大値はGumbel分布に従うこと(パレート分布に従う場合はFréchet分布に従うこと)が数学的に証明されているからです。したがって先行研究の実験結果が正しいとすれば、シナプス遅延の最大値の確率密度分布もこれらの極値分布に漸近すると考えられます。そこで、スパイク信号の決定論的な時間発展モデルである前述のLIFMの時定数に確率的な揺らぎを導入してスパイク信号の時間間隔のランダム性を再現し、単一ニューロンの数値シミュレーションを実施しました。ここで、時定数が指数分布に従えばスパイク信号の時間間隔も指数分布に従います。

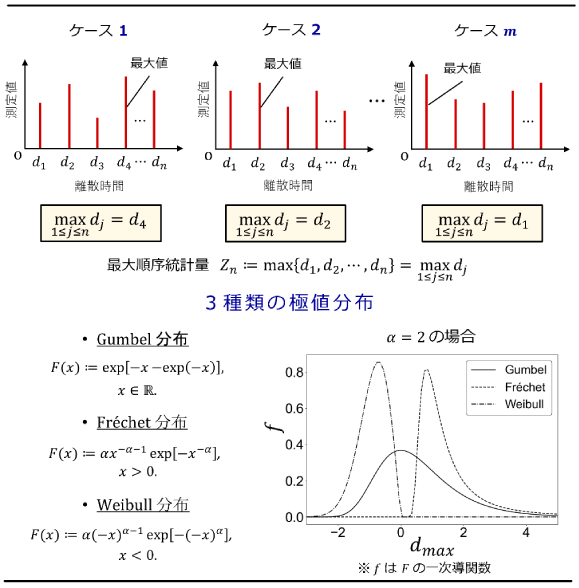
図2:最大順序統計量の考え方(上段)と極値分布(下段)
最大順序統計量の概念図を上段に、3種類の極値分布の具体的な数式と概形を下段に示している。系が確率過程である場合、同じ測定をm回繰り返せば、各ケースでの測定値の最大値も変動する。このとき最大値の漸近分布は、存在するとすれば下段に示した3種類のいずれかの極値分布になることが数学的に知られている。

数値シミュレーションの結果、最大時間間隔の正規化されたヒストグラムは、極値分布のひとつであるGumbel分布に従うことが確認されました(図3参照)。同様にして、スパイク信号の時間間隔がパレート分布に従う場合はFréchet分布に従うことも確認できました。以上の結果は、神経伝達におけるスパイク信号の遅延の最大値の漸近分布は極値分布になることを強く示唆しており、極値理論が神経伝達の遅延の最大値とその頻度を定量的に評価する新しい指標となり得ることを示しています。本研究では単一ニューロンを対象としましたが、より実際の神経ネットワークに近い複数のニューロンが直列や並列に接続される場合に対しても、本研究の成果は比較的容易に拡張できることから、将来において神経ネットワーク全体の記憶や学習の上限(限界)の理論的な推定に役立つことが期待されます。

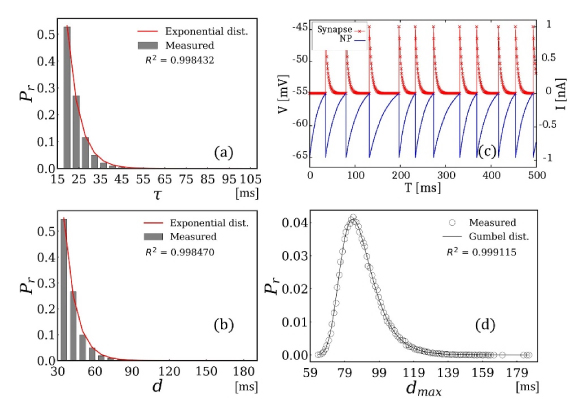
図3:確率的な揺らぎを含むLIFMのシミュレーション値と極値理論に基づく理論値の比較
(a)は時定数、(b)はスパイク信号の時間間隔がそれぞれ指数分布に従う結果を示す。(c)はスパイク信号の波形の例を示している。(d)は最大遅延の正規化されたヒストグラムに対して極値分布のひとつであるGumbel分布関数でフィッティングした結果を示している。