2025-02-06 理化学研究所
理化学研究所(理研)脳神経科学研究センター 数理脳科学研究チームの吉田 健祐 特別研究員、豊泉 太郎 チームリーダーの研究チームは、脳に存在する神経回路構造と脳型のシナプス可塑性学習則[1]を用いて、工学的な非線形次元削減[2]手法と同様の計算を実現する神経回路の数理モデルを提案し、この数理モデルが実際の神経回路の情報処理で活用されている可能性を示しました。
本研究成果は、脳内での複雑な情報処理の解明や脳の神経回路を模したデバイスの開発に貢献すると期待されます。
今回、研究チームは、工学的に有用な非線形次元削減手法の一つであるt-distributed Stochastic Neighbor Embedding(t-SNE)を神経回路の数理モデルで実装したHebbian t-SNEを提案し、t-SNEと同等の性能を発揮することを確認しました。また、ショウジョウバエの嗅覚回路[3]に関連した先行研究の神経活動データの解析により、非線形次元削減が実際の神経回路での情報処理に活用されている可能性を示しました。
本研究は、科学雑誌『Science Advances』オンライン版(2月5日付:日本時間2月6日)に掲載されました。
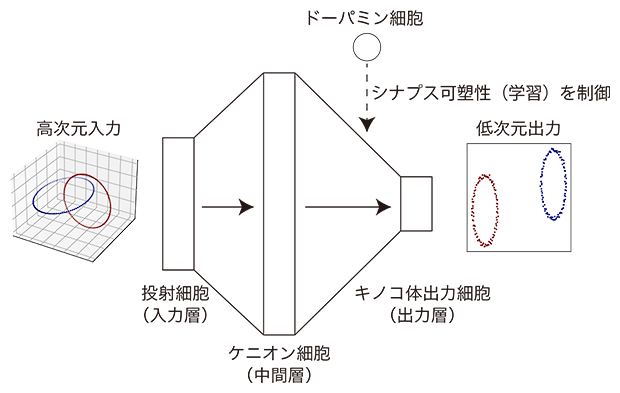
ショウジョウバエ嗅覚回路型の神経回路で非線形次元削減を実現するモデル
背景
複雑な感覚入力を基に効率的に行動を制御するため、脳は高次元の入力を低次元の神経活動へ非線形に変換し、ノイズに対する頑健性や汎化性能[4]を向上させていると考えられています。このような脳の次元削減の仕組みを解明するには、多様な感覚器官からの高次元入力を、神経回路がどのように統合して簡易な低次元表現へと変換するかを明らかにすることが重要です。
一方、機械学習[5]分野で開発されてきたさまざまな次元削減手法は有用性が示されていますが、その多くは神経回路の数理モデルで実装できるか分かっていませんでした。特に、本研究で着目したt-distributed Stochastic Neighbor Embedding(t-SNE)注1)は高次元データの解析において広く使われている非線形次元削減手法ですが、神経回路の数理モデルで実現可能かどうかは明らかになっていませんでした。
注1)van der Maaten L, and Hinton G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(86):2579-2605.
研究手法と成果
研究チームは、代表的な非線形次元削減手法の一つであるt-SNEを入力層・中間層・出力層から成るニューラルネットワーク[6]で近似的に実現するHebbian t-SNEを提案しました。
t-SNEは高次元入力間と低次元出力間のそれぞれの類似度を計算し、二つの類似度を近づけるように低次元出力を変化させることによって、入力構造を捉えた低次元出力を得ます。この計算を神経回路の数理モデルで実現するため、高次元入力X、低次元出力Yに加えて、中間層Zを含むニューラルネットワークを設計しました(図1)。ショウジョウバエの嗅覚回路に関する知見を参考に、XからZへの非線形変換を固定とし、ZからYへのシナプス結合Wの学習則を導く方針としました。本数理モデルではt-SNEにおける類似度を近似的に計算するため、入力・出力の時間変化を利用します。このために、入力がランダムに何度も再生されるような状況を考え、入力・出力の時間変化をグローバルな制御因子Dが比較し、その時間変化の大小関係を一致させるようにWのシナプス可塑性[1]を制御するという補助回路を考えました。その上でt-SNEのアルゴリズムを数学的にうまく変形したところ、Dをグローバルな制御因子としたthree-factor learning rule[7]という脳型のシナプス可塑性に従って、シナプス結合Wを学習する形に書き直せることを見いだし、この書き直したものをHebbian t-SNEと名付けました。
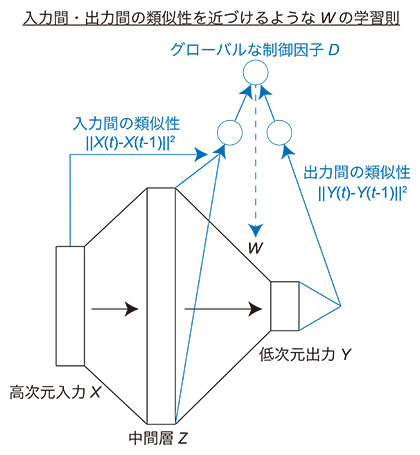
図1 本研究で開発した非線形次元削減の神経回路モデル
高次元入力Xが中間層Zを経て低次元出力Yに変換される。中間層Zから低次元出力Yへのシナプス結合Wが、入力間・出力間の類似性を近づけるようにグローバルな制御因子Dにより制御される。入力間・出力間の類似性は、それぞれ入力・出力の時間変化‖X(t)-X(t-1)‖2、‖Y(t)-Y(t-1)‖2を利用して近似的に計算される。
次に、Hebbian t-SNEがt-SNEと同等の性能を発揮するかを人工データで調べました。線形次元削減手法がうまく働かないような3次元空間で絡んだリング上に並んでいる入力や、機械学習分野で用いられる手書き数字の画像データMNISTにHebbian t-SNEを適用すると、t-SNEと同等の低次元表現が得られ、脳で実行されている可能性が指摘されている他の手法よりも優れた情報表現を学習できました(図2)。
さらに、実際の脳の神経回路でHebbian t-SNEと同様の計算が行われている可能性を、本数理モデルと回路構造が類似しているショウジョウバエ嗅覚回路に着目して、先行研究で測定された神経活動データ注2、3)を用いて検証しました。嗅覚回路で測定された高次元神経活動データにHebbian t-SNEを適用して得られた低次元表現を解析したところ、匂い入力の化学構造に基づく分類をうまく捉えていました。さらに、このようにして得られた低次元表現は、実験的に測定されたショウジョウバエの匂いに対する誘引や忌避の行動データを他手法よりもよく説明していました。これはHebbian t-SNEと同様の計算が、ショウジョウバエの嗅覚回路で行われている可能性を示唆しています。
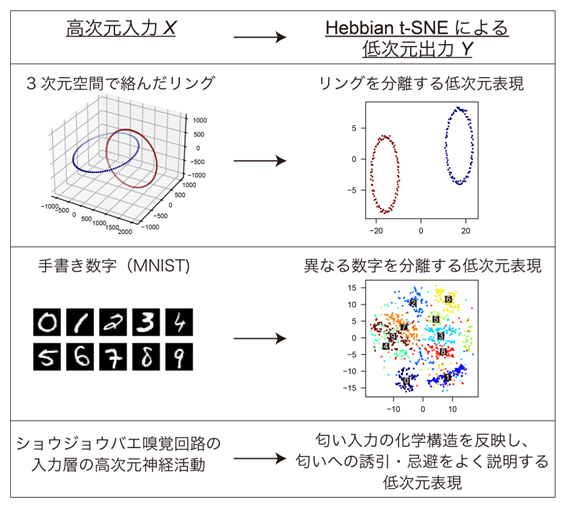
図2 人工データ・ショウジョウバエ嗅覚回路のデータにHebbian t-SNEを適用した結果
Hebbian t-SNEは、絡んだリングを分離した低次元表現、手書き数字の画像(MNIST)で異なる数字を分離したような低次元表現を与える。ショウジョウバエ嗅覚回路の神経活動データに適用しても、匂い入力の化学構造による分類を反映し、実際のショウジョウバエの行動応答をよく説明するような低次元表現を与えた。
このほか、一部の入力に報酬や罰が与えられるような学習に、入力の構造を利用して低次元表現を得るHebbian t-SNEを組み合わせたところ、他の入力に対する報酬や罰を事前に予測することができました。この結果はHebbian t-SNEの高い汎化性能を示しています。
以上の結果は、非線形次元削減が、神経回路の数理モデルでも実現可能であり、脳でも実際に活用されている可能性を示しています。
注2)Hallem EA and Carlson JR. (2006). Coding of Odors by a Receptor Repertoire. Cell, 125(1):143-160.
注3)Badel L, Ohta K, Tsuchimoto Y, Kazama H. (2016). Decoding of Context-Dependent Olfactory Behavior in Drosophila. Neuron, 91(1):155-167.
今後の期待
本研究は、代表的な非線形次元削減手法の一つであるt-SNEと同様の計算を、脳型のシナプス可塑性学習則を用いて実現する脳の神経回路の数理モデル(Hebbian t-SNE)を提案しました。また、Hebbian t-SNEの回路と構造が類似しているショウジョウバエの嗅覚回路において、Hebbian t-SNEと同様な計算が行われている可能性を示しました。Hebbian t-SNEの回路構造は、ショウジョウバエの嗅覚回路に限らず幅広い生物種で観察されます。今後多様な生物種での Hebbian t-SNEの実験的検証が進めば、さまざまな脳機能の解明につながると期待されます。
本研究は、機械学習分野で開発された次元削減手法を脳の情報処理解明へと活用する研究となっており、神経科学分野と近年発展が著しい機械学習分野との融合へのさらなる加速が期待されます。また、Hebbian t-SNEはthree-factor learning ruleというニューロモルフィック計算機[8]と相性の良いものになっており、実際の神経回路を模した計算機・アルゴリズム開発への応用も期待されます。このように、本研究が神経科学分野と機械学習分野の橋渡しとなることにより、双方向で研究が発展することが望まれます。
補足説明
1.シナプス可塑性学習則、シナプス可塑性
神経細胞同士はシナプスという接合部位を介して情報を伝え合うが、その情報伝達効率(シナプス強度)の変化をシナプス可塑性、シナプス可塑性が従う法則をシナプス可塑性学習則と呼ぶ。シナプス可塑性は動物の学習の基盤になっているため、その学習則は高度な情報処理に重要だと考えられている。
2.非線形次元削減
さまざまな特徴を持つ高次元データから、重要な情報を保ちつつ次元数を減らし、データを簡潔にする手法のこと。代表的な手法の一つがt-distributed Stochastic Neighbor Embedding(t-SNE)である。
3.ショウジョウバエの嗅覚回路
ショウジョウバエはモデル動物として広く研究に用いられ、神経活動や行動に関する実験的計測が進んでいる。ショウジョウバエの嗅覚回路は投射細胞・ケニオン細胞・キノコ体出力細胞から成る本数理モデルと類似した回路構造を持つ。
4.汎化性能
既知のデータで学習した後に、新しいデータに正しく対応できる能力。適切な次元削減は入力の重要な部分のみを抽出することで、汎化性能を高める。
5.機械学習
コンピュータがデータ内に潜む構造や規則性を学習し、それを基に予測や判断を行う技術。
6.ニューラルネットワーク
複数の神経細胞がシナプスを介してつながったネットワーク。適切な学習を行うと、ネットワーク全体で高度な情報処理を行うことが可能であることが知られている。
7.three-factor learning rule
シナプス可塑性学習則のうち、(1)そのシナプスの情報を送る側の神経細胞(シナプス前細胞)の活動、(2)受け取る側の神経細胞(シナプス後細胞)の活動、(3)グローバルな制御因子、の三つで記述できるもののこと。脳の神経回路でthree-factor learning ruleに対応するシナプス可塑性が観察されており、脳型のシナプス可塑性学習則と考えられている。
8.ニューロモルフィック計算機
脳の神経回路を模倣して設計された計算機。従来のコンピュータと比較して、エネルギー効率などを向上させることが期待されている。
研究支援
本研究は、科学技術振興機構(JST)戦略的創造研究推進事業(CREST)データ駆動・AI駆動を中心としたデジタルトランスフォーメーションによる生命科学研究の革新(研究総括:岡田康志)「多階層の神経活動データ駆動による睡眠脳の機能解明(研究代表者:井ノ口馨)」、日本学術振興会(JSPS)科学研究費助成事業研究活動スタート支援「リカレントニューラルネットワークを用いた睡眠中の記憶再編成に関する理論研究(研究代表者:吉田健祐)」、同特別研究員奨励費「睡眠中の徐波と神経可塑性の関係に関する理論的研究(研究代表者:吉田健祐)」、孫正義育英財団による助成を受けて行われました。
原論文情報
Kensuke Yoshida, Taro Toyoizumi, “A biological model of nonlinear dimensionality reduction”, Science Advances, 10.1126/sciadv.adp9048
発表者
理化学研究所
脳神経科学研究センター 数理脳科学研究チーム
チームリーダー 豊泉 太郎(トヨイズミ・タロウ)
特別研究員 吉田 健祐(ヨシダ・ケンスケ)
報道担当
理化学研究所 広報室 報道担当