2021-05-18 理化学研究所,慶應義塾大学先端生命科学研究所,北海道大学
理化学研究所(理研)バイオリソース研究センター統合情報開発室の鈴木健大開発研究員、桝屋啓志室長、慶應義塾大学先端生命科学研究所の福田真嗣特任教授、北海道大学大学院先端生命科学研究院の中岡慎治准教授の共同研究グループは、多種の生物がつくる生態系の安定性[1]の変化を俯瞰的に捉えるためのデータ解析手法を開発しました。
本研究成果は、疾患の治療や健康維持、農業技術開発など、多様な分野におけるバイオリソースの新たな利活用につながると期待できます。
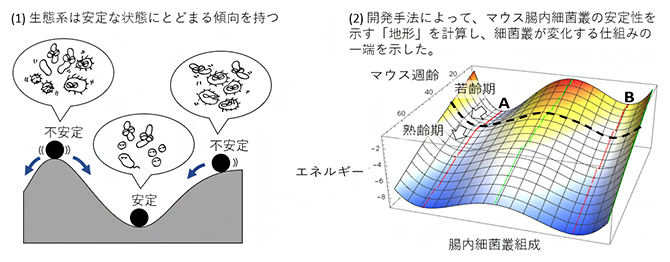
生物の腸内の共生微生物がつくる生態系は、凸凹地形[2]に置かれたボールのように安定状態にとどまる傾向があり、いくつかのタイプに分かれます。この地形が年齢や食生活に伴い変化することで、その安定状態は移り変わります。しかし、これまで生態系の安定性の変化を俯瞰的に捉えることは困難でした。
今回、共同研究グループは、生態系の安定性を表す地形の変化を観測データから推定し、体系的に分析するための手法を開発しました。この手法をマウスの腸内細菌叢データに適用したところ、加齢過程を通じて2通りの安定状態があり、安定状態Aは若齢期に現れやすく、熟齢期にかけて組成[3]が段階的に変化すること、安定状態Bは熟齢期以降にAからBへ変わりやすくなることなどを明らかにしました。この結果は、加齢によりマウスの腸内細菌叢の組成が変化する仕組みの一端を表していると考えられます。
本研究は、科学雑誌『Ecological Monographs』オンライン版(5月12日付)に掲載されました。
加齢に伴うマウス腸内細菌叢組成の安定状態の変化
背景
近年の腸内細菌叢研究では、「エンテロタイプ[4]」と呼ばれる食生活と関連した細菌叢組成など、微生物群集[5]の組成の成り立ちや機能に注目が集まっています。微生物の群集組成の違いは腸内環境の違いを生み出し、その結果ヒトの健康や生活の質に大きな影響を与えることが明らかになっています。そのため、微生物群集組成の変化の予測やコントロールは、医療やヘルスケア分野の重要な課題と考えられています。
さまざまな生物の集まりである微生物群集の共存や安定性は、生態学が古くから扱ってきたテーマです。生物の腸内の共生微生物がつくる群集の組成は、その安定性を地形に例えると、あたかも凸凹地形に置かれたボールのように安定状態にとどまる傾向があります。この「地形」が複数の谷底を持つことは、組成がいくつかのタイプに分かれることを意味し、これが年齢や食生活に伴い変化することで、その安定状態は移り変わります。
生態学では、群集の共存や安定化のメカニズムを理解するためのモデル(ある系の挙動をその主な要素に基づいて記述する数学的な表現)として、古くから「ロトカ-ヴォルテラ方程式[6]」が利用されており、これは腸内微生物群集の研究においても例外ではありませんでした。一方で、近年では次世代シーケンサー[7]などの解析技術の進歩により、現実の微生物群集組成を詳しく測定できるようになりました。
しかし、ロトカ-ヴォルテラ方程式のような生態学の既存モデルでは、こうした観測データから、上で述べたような安定性の変化を捉えることは困難でした。また、しばしば微生物群集組成の解析に利用されるクラスター分析[8]などでは、微生物群集をいくつかのタイプに分けることはできても、それらがなぜ、どのように生じるかを知ることはできませんでした。
「エネルギーランドスケープ[9]解析」を利用することで、微生物群集の安定性をあたかも地形のように把握することが可能になります。この手法は、もともと脳科学分野で提案されたものですが、共同研究グループは解析の基礎となる方程式を拡張することで、安定性の地形が生物をとりまく環境とともにどのように変化するかを推定できるようにし、生態学分野の問題解決に利用するための基盤を整えました。
研究手法と成果
今回、共同研究グループが導入した「拡張ペアワイズ最大エントロピーモデル[10]」では、ある群集組成が生じる確率Pが、環境と生物間相互作用に基づいて複合的に推定されます。複数のサンプル(生態学的群集)から得られる群集組成と環境因子の情報(観測データ)を利用し、モデルのパラメータ[11]を決めることで、観測データに即したモデルが得られます(図1A-C)。このモデルから、全ての群集組成について出現しやすさの指標(エネルギー)を計算でき、安定性を表す地形(エネルギーランドスケープ)が決まります(図1D)。
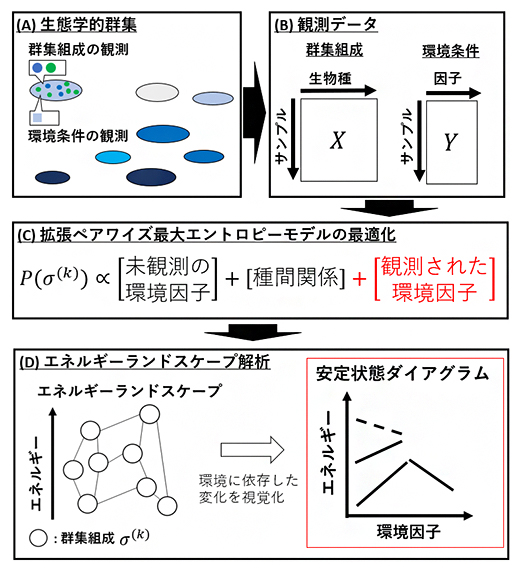
図1 本研究で開発した手法の概要
複数のサンプル(A)から得られる群集組成と環境因子の情報(B)を利用し、モデルのパラメータを決めることで、観測データに即した拡張ペアワイズ最大エントロピーモデル(C)が得られる。Cでは、ある群集組成が生じる確率Pが環境と生物間相互作用に基づいて複合的に推定される。Cから、全ての群集組成について出現しやすさの指標(エネルギー)が計算され、安定性を表す地形(エネルギーランドスケープ)が決まる。Aの楕円はサンプルが得られた環境、丸は微生物種、四角は環境因子を表している。
図2は、拡張ペアワイズ最大エントロピーモデルをマウスの腸内細菌叢に適用することで得られた、加齢に伴う安定性の変化の様子を示しています。データが取得された4週齢から72週齢にわたって、二つの代表的な安定状態AとBが存在しています。安定状態Aは29週齢でTuricibacter、38週齢でBifidobacteriumが加わることで段階的に変化していました。一方で、安定状態Bの時間変化ではこのような組成の移り変わりは見られませんでした。
安定状態Aの前半部分は、加齢に伴う不安定化(エネルギーの上昇)を示す一方で、Bよりも低いエネルギーを持つことからより安定であり、若齢期を代表する組成と考えることができます。この結果は、Lachnospiraceae、Ruminococcaceae、Oscillospiraceaeという3種類の系統分類上近縁な細菌群が、マウスのライフステージの初期段階の腸内環境を特徴づけるというこれまでの報告例とも整合性があります。このようなAの安定性の相対的な高さは加齢とともに失われ、38週齢以降はAとBのエネルギーの違いは小さくなっていました。これは、AB間で遷移しやすくなったことを意味しています。
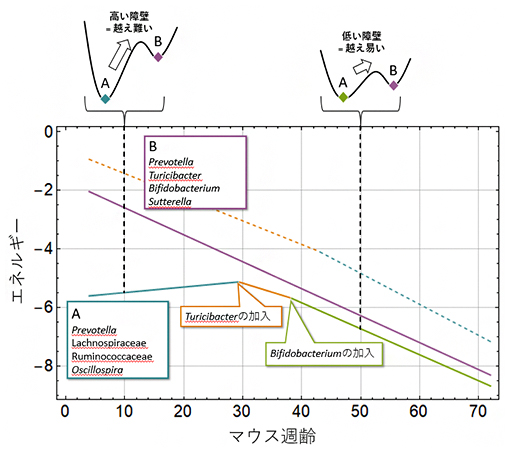
図2 マウス腸内細菌叢の安定状態ダイアグラム
安定状態および分水嶺のエネルギーの加齢に伴う変化。実線が安定状態、破線が分水嶺となる群集組成、各線分の色は群集組成の違いを示している。安定状態について、群集組成をボックスで注釈した。斜体は属、立体は科レベルまで同定された分類群を表している。ダイアグラムの上部に、エネルギーランドスケープの概形を表示した。冒頭の図は、この図と同様のデータからエネルギーランドスケープの変化を曲面で表現したものである。
さらに、ロトカ-ヴォルテラ方程式を用いて微生物群集の動態をシミュレートすることで、開発した手法が実際の安定性の地形とどの程度対応するかを調べました。その結果、さまざまな条件(種数、データ量など)で、実際の安定状態とエネルギーランドスケープの安定状態が一致すること(適合率[12]と再現率[13]の中央値=1)、安定状態の鉢が高い精度で推定できること(適合率と再現率の中央値=0.7~0.9)など、推定されたエネルギーランドスケープが実際の安定性の地形を十分正確に表していることが分かりました。したがって、本手法は、観測データをもとに生態系の安定性を俯瞰的に捉えるための有効な手法であると考えられます。
今後の期待
本研究では、脳神経科学分野で提案されたエネルギーランドスケープ解析と、拡張ペアワイズ最大エントロピーモデルという新しいモデルの導入によって、生態系の安定性の変化を俯瞰的に捉えることができる手法を開発しました。加齢に伴い腸内微生物群集が不安定化することは以前より知られていましたが、本研究は、その仕組みの一端を明らかにしました。一方で、今後より詳しい分析が必要となる結果も示されました。特に、二つの安定状態が宿主にとってどのように違うのかについて、より詳しく理解する必要があります。
この手法からは、群集組成の変化の背後にあるさまざまな安定状態とその結びつきを知ることができます。これは、腸内環境で見られるような、異なる機能を持つ微生物群集組成を結ぶ遷移経路や、そのような遷移を引き起こす微生物、あるいは微生物の組み合わせを特定するために利用できます。こうした情報をもとに実証実験を行うことで、これまで困難と考えられてきた、生物間の複雑な相互作用から成り立つ生態系の操作や、大規模変動の予測のための新しい技術を実現できると考えられます。
今後こうした技術が開発されることで、各分野で研究材料として利用されてきた、微生物、植物、遺伝子などのバイオリソースの新たな利活用法が見いだされるものと期待できます。
補足説明
1.安定性
凹凸地形に置かれたボールは、斜面や山の頂点に比べて谷底に集まりやすい。地形の各点を「生態系が取りうる状態」、ボールを「実現されている状態」とすると、地形上のボールの集まりやすさは、状態の実現されやすさと解釈できる。このような、実現されやすさの程度をここでは安定性と呼ぶ。この解釈では谷底が安定状態となる。
2.地形
本稿全体を通じて、実際の地形ではなく、安定性の高低を表す概念的な地形を指す。
3.組成
ここでは、生物集団を構成する種の在/不在の情報を組成と呼ぶ。種は必ずしも分類学的な種である必要はなく、機能的に等価であるなど、解析上一つの単位と見なすことができる集団を指す。
4.エンテロタイプ
ヒトの腸内細菌群集が示す典型的な組成。主に3タイプに分かれると報告されている。
5.微生物群集
生態系を構成する微生物の集合。微生物群集は動植物の体表面や体内に共生的に定着している他、土壌や海中などさまざまな環境に存在している。ほぼ同じ意味で微生物叢と呼ばれることもある。
6.ロトカ-ヴォルテラ方程式
他の生物や環境からの影響により、生物の存在量がどのように変化するかを表現する数理モデル。微分方程式で表現される。
7.次世代シーケンサー
高度な処理能力を持つ塩基配列の解読装置であり、微生物群集の解析では、サンプルに含まれる塩基配列から数百~数千種を同時に同定するために利用される。
8.クラスター分析
異なる性質のものが混ざり合った集団から、互いに似た性質を持つものを集めてグループに分ける統計的な分析手法。
9.エネルギーランドスケープ
エネルギーランドスケープは、観測データを通じて、実際の生物群集の背後にある安定性の地形を近似する。N種を含む生物群集について、その組成(構成種の在/不在)を表すN個の1または0の配列がその生物群集の「状態」を表すこととする。このとき、この生物群集が取りうる状態は全部で2N個存在する。生物群集の状態変化の最小単位は、このような配列のどれか一つの要素の変化(0が1に、または1が0になる)であるため、それぞれの状態をN個の他の状態と結ぶ。これは一つのネットワークとなる。ここで、各状態にエネルギーを付与したものがエネルギーランドスケープである。エネルギーは状態の出現しやすさの指標であり、エネルギーが低い状態ほど観測されやすく、状態の遷移はエネルギーが低下する方向に起こりやすい。このため、エネルギーランドスケープ上では、直接つながっている他の全ての状態よりエネルギーが低い状態が安定状態となる。
10.拡張ペアワイズ最大エントロピーモデル
微生物種が在/不在の二つの状態のどちらかをとるとき、微生物群集の組成はそれぞれの種の在/不在の配列で表現される。このとき、ペアワイズ最大エントロピーモデルでは、ある組成が生じる確率は、それぞれの種がもともと持っている定着の可能性と、一部の種の間にある協力(互いに同時に存在しやすい)や競争(同時に存在しにくい)といった関係性から決まる。このモデルに、それぞれの種の環境に対する好みを導入したものを、本稿では拡張ペアワイズ最大エントロピーモデルと呼ぶ。
11.パラメータ
最尤法(さいゆうほう)により推定されたパラメータは、各種がその生起において、他種や環境要因から受ける影響の正負やその大きさを表しており、種レベルの特徴が群集レベルの環境応答にどのような役割を果たしているかを理解するために利用できる。
12.適合率
エネルギーランドスケープ上で安定状態であった群集組成のうち、実際の安定性地形においても安定状態であったものの割合。
13.再現率
実際の安定性地形において安定状態であった群集組成のうち、エネルギーランドスケープにおいても安定状態であったものの割合。
研究支援
本研究は、JSPS科研費 JP20H03010, JP20K06820による支援を受けて行われました。
原論文情報
Kenta Suzuki, Shinji Nakaoka, Shinji Fukuda, Hiroshi Masuya, “Energy landscape analysis elucidates the multistability of ecological communities across environmental gradients”, Ecological Monographs, 10.1002/ecm.1469
発表者
理化学研究所
バイオリソース研究センター 統合情報開発室
開発研究員 鈴木 健大(すずき けんた)
室長 桝屋 啓志(ますや ひろし)
慶應義塾大学先端生命科学研究所
特任教授 福田 真嗣(ふくだ しんじ)
北海道大学 大学院先端生命科学研究院
准教授 中岡 慎治(なかおか しんじ)
報道担当
理化学研究所 広報室 報道担当
慶應義塾大学先端生命科学研究所 渉外担当 日野、塩澤
北海道大学 総務企画部広報課 広報・渉外担当