2022-06-01 理化学研究所
理化学研究所(理研)生命機能科学研究センター生体非平衡物理学理研白眉研究チームの足立景亮基礎科学特別研究員(数理創造プログラム基礎科学特別研究員)、理研数理創造プログラムの入谷亮介研究員、濱崎立資上級研究員(開拓研究本部濱崎非平衡量子統計力学理研白眉研究チーム理研白眉研究チームリーダー)の研究チームは、情報理論・統計物理学[1]の手法を用いることで、進化・生態系の個体群ダイナミクス[2]を扱う理論モデルにおいて幅広く成り立つ関係式を提案しました。
本研究成果は、進化や生態系における複雑な個体数の時間的変化を統一的枠組みによって理解することにつながると期待できます。
個体ないし遺伝子に係る自然選択や遺伝子の突然変異に伴う進化、および個体間の捕食・被食や競合関係を伴う生態系では、個体数の時間的変化(個体群ダイナミクス)が起こります。一般に、進化や生態系の個体群ダイナミクスは複雑であり、個体間の相互作用などに起因した非線形[3]性を含む理論モデルで表現されると考えられています。しかしこれまで、このような複雑な個体群ダイナミクスにおいて、一般に成り立つ関係式が存在するのかどうかは不明でした。
今回、研究チームは、統計物理学の方法を応用することで、個体群ダイナミクスにおいて一般的に成り立つ関係式(速度限界不等式)を提案し、この関係式が幅広い進化・生態系のモデルで成立することを検証しました。
本研究は、オンライン科学雑誌『Communications Physics』(6月1日付:日本時間6月1日)に掲載されました。
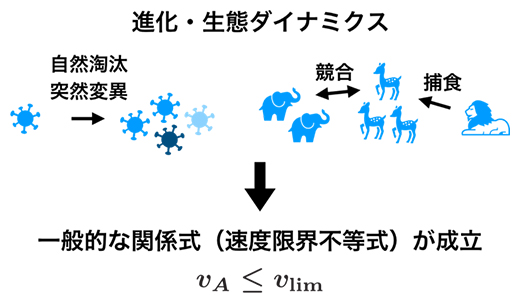
幅広い進化・生態ダイナミクスで成立する速度限界不等式(vA:変化速度、vlim:速度限界)
背景
自然界では、生物の個体数が時間の経過とともにしばしば複雑に変化します(個体群ダイナミクス)。個体群ダイナミクスの背景にあるメカニズムを知ることは、生物の進化や生態系を理解する上で重要な手掛かりとなります。
生物進化の例として、一つの種から異なる種が出現する「種の分化」があります。これは、同種の集団の中である特徴を持った個体の割合が広がっていくことで生じ、自然選択や遺伝子の突然変異が重要な役割を果たしていると考えられています。自然選択は、増殖率の大きな遺伝子型を持つ個体(他の個体よりも多くの子孫を残せる個体)が出現したとき、その頻度を増やす役割を果たします。特に自然選択の影響のみを考えたとき、さまざまな遺伝子型を持つ個体から成る集団の平均的な増殖率の時間的変化は、増殖率の個体間のばらつきに比例する(個体群の増殖率の増加は、遺伝的な多様性の高さで決まる)という「フィッシャーの基本定理[4]」が知られており、進化理論における基本的な関係式となっています。
また、生態系では、捕食・被食や競合を通して個体間に相互作用が生じることに起因して、個体群ダイナミクスを記述する理論モデルは非線形になります。このような非線形性は、例えば個体数の急激な変化や時間的な振動を説明するのに主要な役割を果たしていると考えられています。
フィッシャーの基本定理は突然変異がある場合には適用できず、また生態系では非線形性によって現象が複雑化するため、系を特徴づける多様度[5]のような量に対して一般に成り立つ関係式を見つけるのは困難でした。そのため、このような一般的な関係式が見つかれば、複雑な進化・生態ダイナミクスを統一的視点から説明できるようになると考えられます。
そこで本研究では、進化や生態系の非線形な個体群ダイナミクスにおいて、突然変異の影響や、増殖率以外の量も考慮した一般的な関係式は存在するのかという問いを考えました。
研究手法と成果
研究チームはまず、ランダムウォーク[6]を代表とする確率的ダイナミクスと進化・生態系における個体群ダイナミクスの類似性に注目しました(図1)。ランダムウォークは、統計的には粒子位置の確率分布の時間的変化として記述できます(図1左)。一方、あるタイプ(遺伝子型、表現型、あるいは種)の個体数を全個体数で割った量を頻度と呼ぶと、個体群ダイナミクスは統計的には各タイプの頻度の時間的変化として記述できます(図1右)。確率的ダイナミクスで確率の総和がどの時刻でも1になるのと同様に、個体群ダイナミクスでは頻度の総和が常に1になります。
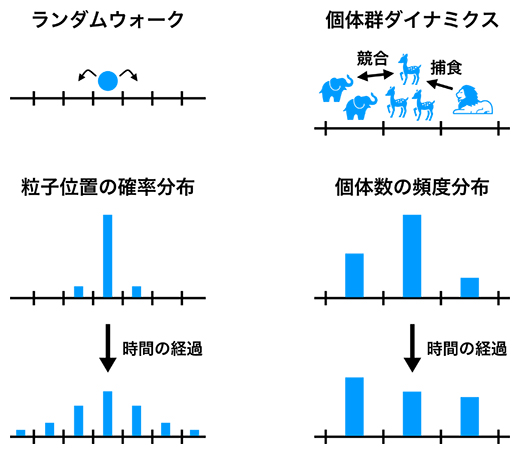
図1 確率的ダイナミクスと個体群ダイナミクスの類似性
(左)確率的ダイナミクスの代表例であるランダムウォークの模式図。最初に直線上の中央にあった粒子(青丸)は、確率的に左右どちらかに移動するものとする。時間の経過とともに粒子位置の確率分布(棒グラフの高さで示す)は変化するが、「直線上のどこか」にいる確率は必ず1である。
(右)進化・生態系の個体群ダイナミクスの例として、複数のタイプ(ここでは三つの種)から成る生態系を表した模式図。棒グラフは、生態系の全個体数における各種個体数の割合(頻度)を示す。時間の経過とともにそれぞれの種の個体数の頻度分布が変化するが、頻度の総和は必ず1となる。
近年の統計物理学の研究により、確率的ダイナミクスでは、物理量の変化速度に一般的な上限が存在し、変化速度がある不等式を満たすことが明らかにされてきました注1、2)。この不等式は、確率の総和が1になることから導かれます。そこで、統計物理学の知見を利用し、確率の代わりに頻度を考えることで、個体群ダイナミクスにおける変化速度が満たす不等式(速度限界不等式)を一般に成り立つ関係式として得ることができました。速度限界不等式は、増殖率を含む一般的な量の変化速度(vA)が速度限界(vlim)を持つことを意味し、自然選択や遺伝子の突然変異を伴う進化について成り立つほか、生態系の多様度を表すエントロピー[7]の変化速度にも適用できます(図2)。
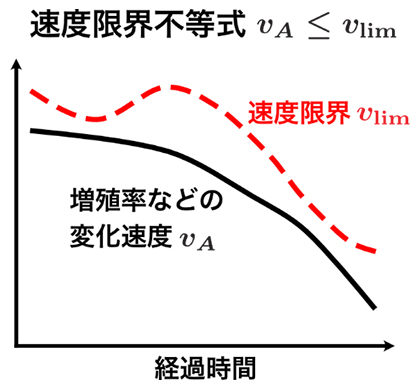
図2 速度限界不等式の概念図
速度限界不等式によれば、増殖率やエントロピーといった量の変化速度vAは、速度限界vlim以下の値をとる。速度限界の値は経過時間に依存するが、変化速度は常に速度限界以下の値となる。
次に、特別な場合として、突然変異のない進化の理論モデルを考え、速度限界不等式を増殖率に対して適用しました(図3)。その結果、不等式は等号を満たして等式になることが分かり、さらにこの等式を変形すると、フィッシャーの基本定理が得られることが分かりました。つまり、本研究で議論した速度限界不等式は、フィッシャーの基本定理を一般化した関係式であることが明らかになりました。

図3 速度限界不等式と既存の関係式との関係
速度限界不等式は、幅広い進化・生態ダイナミクスにおいて、一般の量に対して成り立つ(vA:一般の量の変化速度、vlim:速度限界)。一方、既存の関係式(フィッシャーの基本定理;∂t〈s〉:増殖率の時間変化、(Δs)2:増殖率の個体間のばらつき)は、突然変異のない進化ダイナミクスにおいて、増殖率に対して成り立つ。フィッシャーの基本定理は、等号を満たす速度限界不等式(vs:増殖率の変化速度、vlim:速度限界)と等価であるため、速度限界不等式はフィッシャーの基本定理の一般化と見なせる。
さらに、突然変異のある進化の理論モデルや感染症の理論モデル、競合する生態系の理論モデルといった幅広い非線形の進化・生態系モデルにおいて、速度限界不等式が確かに成立していることを数値計算および解析的計算により検証しました(図4)。このようなモデルでは、増殖率や突然変異率などのパラメータが変化することで、種の絶滅や感染症の蔓延といった劇的な変化が起こります。このような変化が起こる点は「分岐点」と呼ばれます。
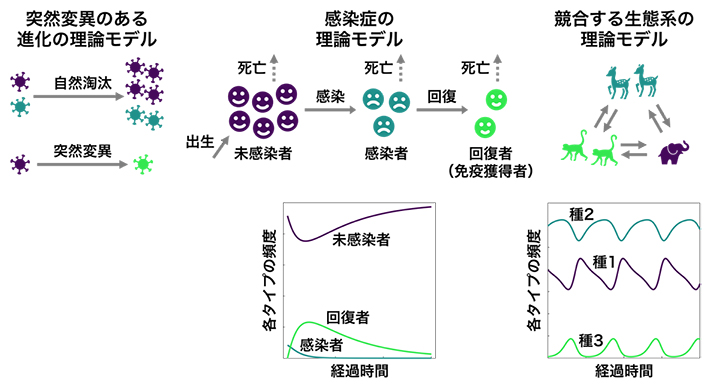
図4 速度限界不等式が成立するさまざまな非線形の進化・生態系モデル
上)速度限界不等式が成立することが検証された理論モデルの例。速度限界不等式は、フィッシャーの基本定理では扱わない突然変異のある進化モデルでも成り立つ(左)。また、未感染者・感染者・回復者のダイナミクスを扱う感染症の理論モデル(中)や、競合する複数種の個体群ダイナミクスを扱う生態系の理論モデル(右)にも適用できる。
下)理論モデルに従う個体群ダイナミクスの例。感染症モデルでは感染力の強さなどがパラメータとなり、図(左)のように短期間のうちに感染が収束する場合もあるが、劇的な蔓延に向かうパラメータの分岐点が存在する。ある種の個体数変化が別の種の個体数変化に影響する生態系モデル(右)では、増殖率などがパラメータとなり、頻度が時間的に振動するか、時間変化のない安定状態(絶滅を含む)に落ち着くかのパラメータの分岐点が存在する。
分岐点の近くでは、モデルの詳細に依存しない「スケーリング則[8]」と呼ばれる関係式が成り立ちます。分岐点の近くで成り立つスケーリング則に速度限界不等式を適用したところ、スケーリング則の形に一般的な制限(指数に関する不等式)が存在することが分かりました(図5)。この制限は分岐のタイプのみに依存し、系の詳細には依存しないという意味で普遍的であり、多様な進化・生態ダイナミクスにおいても成立すると考えられます。
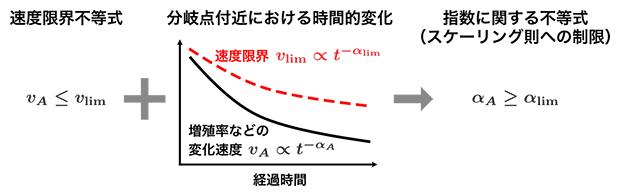
図5 スケーリング則への制限の例
速度限界不等式(左)を分岐点の近くで成り立つスケーリング則(中;時間やパラメータの変化に対する関数関係)に適用すると、スケーリング則に対する一般的な制限として指数に関する不等式(右)が導かれる。
注1)S. Ito and A. Dechant, Stochastic time evolution, information geometry, and the Cramér-rao bound, Phys. Rev. X 10, 021056 (2020).
注2)S. B. Nicholson, L. P. García-Pintos, A. del Campo, and J. R. Green, Time-information uncertainty relations in thermodynamics, Nat. Phys. 16, 1211 (2020).
今後の期待
本研究により、幅広い進化・生態系の理論モデルで成り立つ関係式が明らかになりました。この関係式は、統計物理学の近年の研究を応用することで得られたものであり、これまで進化理論で知られていた基本的な関係式を大きく一般化するものです。
従来、生態学や進化学の理論的手法は、それぞれほぼ独立に確立されてきました。本成果は、進化や生態系における複雑な個体群ダイナミクスを統一的な枠組みによって説明することにつながると期待できます。また、理論生物学と情報理論や理論物理学という異分野を結びつけ、包括的アプローチによる生物現象のさらなる解明を促進すると考えられます。
補足説明
1.統計物理学
系を構成する要素の性質に基づき、要素集団の巨視的な性質を導くための学問。
2.個体群ダイナミクス
ある範囲に生息する同一種からなる集団を個体群と呼ぶ。個体群ダイナミクスは、個体群を構成する個体数の時間変化を指す。
3.非線形
数理モデル(微分方程式)において、変数を定数倍したとき、式の形が変わらないモデルを線形モデルと呼び、式の形が変わるモデルを非線形モデルと呼ぶ。
4.フィッシャーの基本定理
集団遺伝学の創始者の一人である英国のロナルド・フィッシャーが、1930年出版の『The Genetical Theory of Natural Selection』で発表した遺伝的変異に関する定理。「ある時点での生物の適応度の増加率は、その時点での適応度の遺伝的分散に等しい」と表現される。
5.多様度
さまざまな生物種が共存しているときに、種の多様性の度合いを表す指標。
6.ランダムウォーク
粒子がある位置から別の位置に動く際に、どの位置に動くのかが確率的に決定されるような運動。
7.エントロピー
ここでは、シャノンのエントロピー(情報エントロピー)を指し、生物種の多様性を数値化する指標の一つ。
8.スケーリング則
注目している量の尺度(スケール)を変えたとき、複数の量の間に成り立つ普遍的な関係式。例えば、球の半径と体積の間の関係や、ランダムウォークにおける経過時間と平均二乗変位の間の関係など。
研究チーム
理化学研究所
生命機能科学研究センター 生体非平衡物理学理研白眉研究チーム
基礎科学特別研究員 足立 景亮(アダチ・キョウスケ)
(数理創造プログラム 基礎科学特別研究員)
数理創造プログラム
研究員 入谷 亮介(イリタニ・リョウスケ)
(東京大学 大学院理学系研究科 生物科学専攻 客員研究員)
上級研究員 濱崎 立資(ハマザキ・リュウスケ)
(開拓研究本部 濱崎非平衡量子統計力学理研白眉研究チーム 理研白眉研究チームリーダー)
研究支援
本研究は、理化学研究所運営費交付金(理研白眉)で実施し、日本学術振興会(JSPS)科学研究費補助金若手研究「接着性培養細胞を用いた非平衡協同現象における普遍性の探索(研究代表者:足立景亮)」「被子植物におけるゲノム刷り込みと胚乳の倍数性の進化維持機構を解明する理論研究(研究代表者:入谷亮介)」、同研究活動スタート支援「寄生者による宿主操:その適応進化動態と食物網動態の間のフィードバック構造の解明(研究代表者:入谷亮介)」、同挑戦的研究(萌芽)「宿主操作の分子・神経メカニズムから解き明かす生態系のエネルギー流(研究代表者:佐藤拓哉)」、iTHEMS「情報理論スタディグループ」による支援を受けて行われました。
原論文情報
Kyosuke Adachi, Ryosuke Iritani, and Ryusuke Hamazaki, “Universal constraint on nonlinear population dynamics”, Communications Physics, 10.1038/s42005-022-00912-4
発表者
理化学研究所
生命機能科学研究センター 生体非平衡物理学理研白眉研究チーム
基礎科学特別研究員 足立 景亮(アダチ・キョウスケ)
(数理創造プログラム 基礎科学特別研究員)
数理創造プログラム
研究員 入谷 亮介(イリタニ・リョウスケ)
上級研究員 濱崎 立資(ハマザキ・リュウスケ)
(開拓研究本部 濱崎非平衡量子統計力学理研白眉研究チーム 理研白眉研究チームリーダー)
報道担当
理化学研究所 広報室 報道担当