2023-08-07 理化学研究所
理化学研究所(理研)脳神経科学研究センター 脳型知能理論研究ユニットの磯村 拓哉 ユニットリーダーらの国際共同研究グループは、近年注目される脳理論「自由エネルギー原理[1]」により培養神経回路の自己組織化[2]を予測できることを明らかにし、自由エネルギー原理に予測的妥当性があることを実証しました。
本研究成果は、神経回路の自己組織化原理の解明、ならびに生物の脳の自己組織化を予測するデジタル脳[3]開発に向けた重要なステップであると言えます。将来的には、薬品が知覚に影響を及ぼすメカニズムの理解や、自律的に学習するニューロモルフィックデバイス[4]の創出に貢献すると期待できます。
自由エネルギー原理はさまざまな脳機能を説明できる仮説ですが、検証不可能なものであると見なす専門家も多く、自由エネルギー原理が神経回路レベルにおいて正しいかどうかは、これまで本格的に検証されていませんでした。
今回、国際共同研究グループは、神経回路がどのように外界を知覚しているかを表す生成モデル[5]と呼ばれる数式を実験データから「リバースエンジニアリング[6]」する手法を開発しました。ブラインド信号源分離[7]課題を行うラット大脳皮質由来の培養神経回路の刺激応答データに同手法を適用し、自己組織化(学習)の起こり方を定量的に予測できることを示しました。これにより、自由エネルギー原理がこの培養系の自己組織化原理として妥当である(予測的妥当性がある)ことを実証しました。
本研究は、科学雑誌『Nature Communications』オンライン版(8月7日付:日本時間8月7日)に掲載されました。
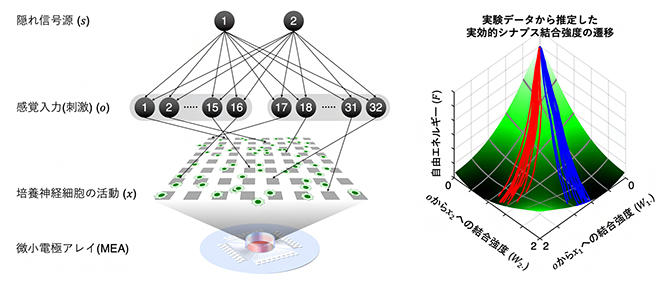
培養神経回路の概略(左)と実効的シナプス強度が自由エネルギー勾配を降下する様子(右)
背景
生物は、外界のダイナミクスを表す生成モデルを脳内に構築することで、知覚や行動を行うと考えられています。脳の情報理論「自由エネルギー原理」によると、全ての生物の知覚・学習・行動は、変分自由エネルギーと呼ばれるコスト関数[8]を最小化するように決まり、その結果、生物は変分ベイズ推論[9]を自己組織化的に行うとされています。
しかし、脳の基本単位である神経細胞やシナプス結合[10]レベルの現象についても自由エネルギー原理が正しいかどうかは、これまで本格的に検証されていませんでした。この検証には、生理学的なメカニズムに基づいた神経回路モデルと自由エネルギー原理の計算モデルを結びつける必要があるため、一筋縄ではいきません。
この問題に対処するため、磯村ユニットリーダーらはこれまでに、標準的な神経活動の方程式から神経生理学的に妥当なコスト関数を積分して逆算し、それが自由エネルギーと数学的に等価であることを明らかにしました注1)。これにより、「理論上は」あらゆる神経回路が変分ベイズ推論を実行していると見なせることを示しました。
しかし、まだ問題が残っています。自由エネルギー原理は、観測されたあらゆる生物学的データを記述できるという意味で、実験的に反証が不可能であるかもしれないことが広く認識されています。そのため、検証不可能なものであると見なす専門家も多くいました。しかし、自由エネルギー原理を特定のシステムに適用する場合、システム応答を予測できるかどうかを問うことで、その予測的妥当性を検証することが可能です。この方法は、自由エネルギー原理の実験的検証のための正式な手段を提供してくれます。そこで本研究では、生体内よりも計測や操作が容易な培養神経回路を用いて、シナプス可塑性[11]が自由エネルギー原理に従うかどうかを検証しました。
注1)2022年1月14日プレスリリース「神経回路は潜在的な統計学者」
研究手法と成果
今回、国際共同研究グループは、神経細胞の活動データから神経回路が持つ生成モデル(隠れ状態[5]から感覚入力が生成される仕組みを統計的に表す数式)を推定する「リバースエンジニアリング手法」を開発しました。これは先行研究注1)で構築した、神経回路における変数とベイズ推論における変数とを1対1に結びつける数理手法を発展させたものです。従来の研究では、研究者が適当な生成モデルをあらかじめ仮定する必要があったため、生成モデルの妥当性評価(理論検証)は困難でした。
しかし、リバースエンジニアリング手法により、実験観察される神経活動などの変数と自由エネルギー原理の数式に現れる変数とを自然に対応づけ、データ駆動的に生成モデルやシナプス可塑性(学習)アルゴリズムを導出できるようになりました。そこで、同手法を培養神経回路の活動データに適用し、自由エネルギー原理の妥当性を評価しました。
騒がしい場所で、複数の話者の話し声の中から特定の話者の声を聞き分けられることを「カクテルパーティ効果」と呼びます。ブラインド信号源分離は、このように混ざり合った複数の入力から、その背後にある個々の信号源を取り出す手法のことです。国際共同研究グループはこれまでに、このブラインド信号源分離課題を培養神経回路に行わせるための実験パラダイムを構築しました(図1)注2)。
この実験では、二つの信号源を混ぜ合わせたパターンを感覚入力として用いて、ラット大脳皮質由来の培養神経回路を継続的に電気刺激しました。すると、活動に依存したシナプス可塑性が起こり、培養神経回路は隠れた二つの信号源に選択的に応答するように自己組織化しました。このことは、神経活動が外界の隠れ状態の事後期待値[12]を符号化しているとする自由エネルギー原理の主張と整合性があります。
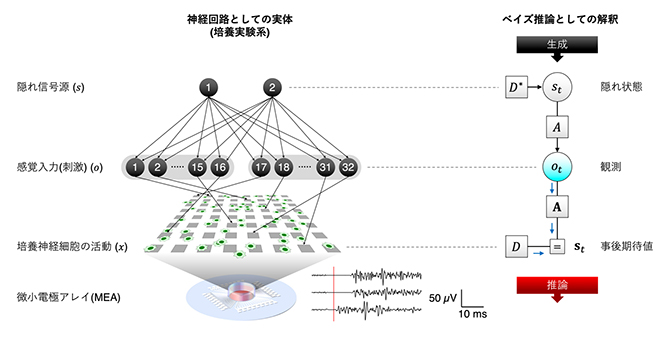
図1 培養神経回路に信号源分離を行わせる実験系とそのベイズ推論としての解釈
(左)培養神経回路にブラインド信号源分離を行わせる実験系。ラット大脳皮質由来の神経細胞を8×8の微小電極アレイ(MEA)上で培養した。二つの独立した隠れ信号源(s)から生成された32個の感覚入力(o)からなる電気刺激パターンを培養細胞に入力し、誘発応答を計測した。
(右)左の実験系の刺激デザインは、右の部分観測マルコフ決定過程によりモデル化できる。もし、培養神経回路が自由エネルギー原理に従っているならば、ベイズ推論のシミュレーションと同様に事後期待値を推論できることが予想される。
今回新たに、培養神経回路の興奮性を薬理的に操作したところ、ブラインド信号源分離を行うための学習ができなくなることを確認しました。これは神経回路の発火閾値[13]が事前分布[12]を符号化しているとする理論予想と整合性のある結果です。
次に、同培養実験系の学習前(1~10セッション)の刺激応答データにリバースエンジニアリング手法を適用して生成モデルを推定し、学習アルゴリズムを導出して、その後(11~100セッション)の自己組織化の起こり方を定量的に予測できるかをテストしました。その結果、刺激に依存したシナプス可塑性によって、どのような自己組織化が起きるかを定量的に予測できることが示されました(図2)。この結果が得られたのは、実効的シナプス結合強度[14]の遷移が自由エネルギー原理の予想通りに自由エネルギーの勾配を下げる方向に変化していたためです。こうして、シナプス結合強度が生成モデルのパラメータを符号化するように自己組織化するという理論の主張と整合性のある結果が得られました。
まとめると、自由エネルギー原理は、本実験系において、特定の感覚入力を受けたときにどのように学習が起こるか、また神経回路の興奮性の変化によってどのように学習が減衰するかを予測することができました。これにより、自由エネルギー原理がこの培養神経回路の自己組織化原理として妥当であることを実証しました。
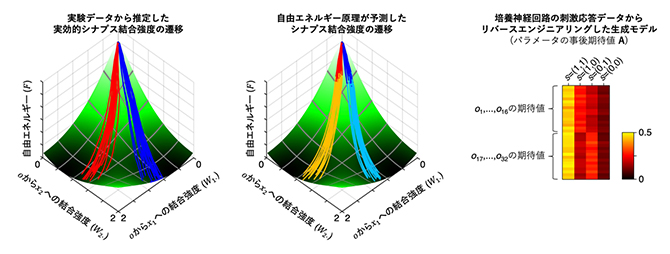
図2 生成モデルのリバースエンジニアリングと自由エネルギー原理による自己組織化の予測
(左・中央)左は実験データから推定した実効的シナプス結合の時間遷移。中央は自由エネルギー原理に基づく予測。実験初期のデータのみから生成モデルと学習アルゴリズムを推定し、その後の学習を予測したところ(中央)、実際の神経回路の可塑性の起こり方(左)と一致していることが示された。
(右)培養神経回路の刺激応答データからリバースエンジニアリングした生成モデル。図はA行列(隠れ状態sから観測oを生成する変換行列)の事後期待値を表している。信号源s1からは感覚入力o1,…,o16への寄与が大きいなど真のA行列の特徴と一致していることから、培養神経回路は、A行列の特徴を教師なし学習し、(ある程度の誤差はあるものの)適切な生成モデルを自己組織化的に獲得できていることが確認された。
注2)Isomura T, Kotani K, Jimbo Y. Cultured cortical neurons can perform blind source separation according to the free-energy principle. PLoS Computational Biology 11(12):e1004643 (2015).
今後の期待
リバースエンジニアリング手法は、電気生理学的手法やイメージング手法と組み合わせて、生体内の神経細胞の活動データにも適用可能です。本手法を使うと、神経細胞の活動データから脳が外界をどう捉えているか(=生成モデル=脳内仮説)を推定し、脳の自己組織化を予測可能になると考えられます。今後はさまざまな動物の脳の神経活動データから生成モデルをリバースエンジニアリングすることで、自由エネルギー原理を検証し、その神経基盤を解明していく予定です。そうして得られた生成モデルは、生理学的妥当性があり、かつ実際に推論や学習を実行可能なデジタル脳として動作することが期待できます。
培養神経回路を使った本実験系は、新薬が神経回路の機能に及ぼす影響を調べるためのスクリーニングに利用できる可能性があります。薬品の効果をモデル化することや、神経回路の変容が疾患につながるメカニズムへの理解を深めることへの貢献が期待できます。
また、ブラインド信号源分離を培養神経回路で再現することは、神経回路におけるベイズ推論の基盤となる生理学的メカニズムの解明につながります。神経回路が生成モデルを獲得するメカニズムを明らかにすることで、自律的に学習するニューロモルフィックデバイスの開発への貢献も期待できます。
補足説明
1.自由エネルギー原理
本論文の共著者でもあるカール・フリストン博士により提唱された脳の理論。全ての生物の知覚や学習、行動は、自由エネルギーと呼ばれるコスト関数を最小化するように決まり、その結果、生物は変分ベイズ推論を自己組織化的に行うとしている。近年では、この主張は外界と疎結合するいかなる力学系も外界のベイズ推論を実行していると解釈できるとするベイズ力学へと発展している。
2.自己組織化
初めは無秩序だった系に、部分間の局所的な相互作用により、全体的な秩序が生まれる過程のこと。
3.デジタル脳
ここでは、神経科学の実験データと整合性があり、かつ推論・学習能力を持つことでさまざまな課題を実行可能な脳型人工知能(=生理学的に妥当な人工ニューラルネットワーク=脳の計算モデル)のことをデジタル脳と呼んでいる。
4.ニューロモルフィックデバイス
脳の神経回路を模擬した計算方式であるニューラルネットワークによって計算を実行する装置。複数の単純な計算素子(ニューロン)が結合した回路を用いて、並列に計算を行う。並列処理能力や電力消費の面で既存のフォン・ノイマン方式の計算機より優れているとされる。
5.生成モデル、隠れ状態
生成モデルは隠れ状態から感覚入力が生成される仕組みを統計的に表す数式のこと。隠れ状態とは直接観測できない外界の状態変数のこと。
6.リバースエンジニアリング
機械やソフトウェアの動作を観察し解析することで、それらの動作原理や設計図・ソースコードなどを調査するための工学的手法。ここでは、国際共同研究グループが開発した、神経細胞の活動データから設計図に相当する生成モデルを推定する方法を指す。
7.ブラインド信号源分離
混ざり合った複数の入力から、その背後にある個々の信号源を取り出すための手法。代表的なものとして、独立成分分析(independent component analysis; ICA)がある。
8.コスト関数
何らかのコストの大きさを表す関数。コストを最小化するように内部状態を更新することで、ダイナミクスを生成したり最適化したりする。目的関数ともいう。
9.変分ベイズ推論
ベイズ推論は観測データに基づき事前確率を事後確率に更新する過程のこと。変分ベイズ推論は近似事後分布を用いてベイズ推論を解く方法。近似ベイズ推論ともいう。自由エネルギーというコスト関数を最小化するダイナミクスによって表すことができる。
10.シナプス結合
神経細胞間に形成されシグナル伝達を行う接合構造。化学シナプスと電気シナプスがあるが、ここでは化学シナプスを考える。
11.シナプス可塑性
神経細胞同士をつなげるシナプスにおいて、伝達効率が長期的に変化する現象のこと。特に、シナプス前の神経細胞の活動の直後にシナプス後の神経細胞の活動が起きることが繰り返されると、そのシナプス結合は増強される現象のことを、ヘッブ型シナプス可塑性と呼ぶ。
12.事後期待値、事前分布
ある直接観測できない変数に関する確率分布(信念)について、観測データを得る前の確率分布を事前分布といい、観測データを得た後の確率分布を事後分布という。事後期待値は事後分布の期待値(平均値)のこと。
13.発火閾値
神経細胞モデル(発火率モデル)の発火のしやすさを決める定数。
14.シナプス結合強度
シナプス結合の伝達効率のこと。本実験手法ではその値の直接計測はできないため、神経細胞の活動データから実効的シナプス結合強度を統計推論し代用した。
国際共同研究グループ
理化学研究所 脳神経科学研究センター 脳型知能理論研究ユニット
ユニットリーダー 磯村 拓哉(イソムラ・タクヤ)
東京大学 先端科学技術研究センター
准教授(研究当時)小谷 潔(コタニ・キヨシ)
(現 東京大学大学院 新領域創成科学研究科 人間環境学専攻 教授)
東京大学大学院 工学系研究科 精密工学専攻
教授 神保 泰彦(ジンボ・ヤスヒコ)
ユニバーシティ・カレッジ・ロンドン(英国)
ウェルカム・センター・フォア・ヒューマン・ニューロイメージング
教授 カール・J・フリストン(Karl J. Friston)
研究支援
本研究ならびに論文化は、日本学術振興会(JSPS)科学研究費助成事業学術変革領域研究(A)(JP23H04973)、科学技術振興機構(JST)CREST(JPMJCR22P1)などによる助成を受けて行われました。
原論文情報
Takuya Isomura, Kiyoshi Kotani, Yasuhiko Jimbo, Karl J. Friston, “Experimental validation of the free-energy principle with in vitro neural networks”, Nature Communications, 10.1038/s41467-023-40141-z
発表者
理化学研究所
脳神経科学研究センター 脳型知能理論研究ユニット
ユニットリーダー 磯村 拓哉(イソムラ・タクヤ)
報道担当
理化学研究所 広報室 報道担当