低次元空間上でフローサイトメトリーの時系列動画も再現
2020-04-15 京都大学
岡田大瑚 医学研究科博士課程学生、山田亮 同教授は、複雑な確率分布に幾何的な座標を与える新規の統計手法であるDEEF法を開発し、細胞集団プロファイルの違いや変化を定量・可視化することに成功しました。
生体内の細胞1つ1つのタンパク質や遺伝子の発現量はどれも同じではなく少しずつ違っているため、その細胞集団全体としての性質はこれらの細胞集団が作る分布として特徴づけることができます。このような分布は、細胞1つ1つに発現している遺伝子やタンパク質量を多数の細胞について測定する1細胞発現解析によって測定することができます。一方で、情報科学の分野では、確率分布同士の違いを幾何学的に研究する情報幾何学が発展してきました。
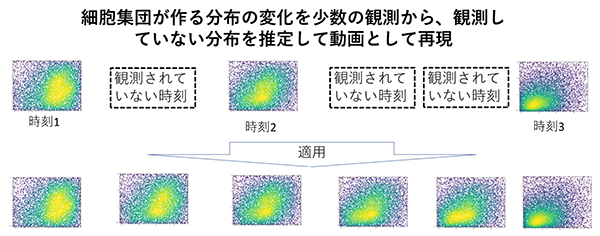
本研究では、1細胞発現データのような複雑な分布に対して情報幾何的な座標を与え、ぞれぞれの座標が説明するパターンを抽出する新しい統計手法を開発し、細胞集団プロファイルの違いや変化を低次元空間上で定量・可視化することに成功しました。この手法の応用例としては、経時的に観測したフロサイトメトリーデータから、観測時刻と観察時刻の間の分布状態を推測し、動画を再構成することが挙げられます。
本研究成果は、2020年4月11日に、国際学術誌「PLOS ONE」のオンライン版に掲載されました。
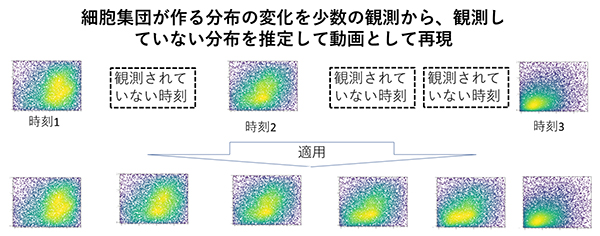
図:本研究の概要図
書誌情報
【DOI】 https://doi.org/10.1371/journal.pone.0231250
【KURENAIアクセスURL】http://hdl.handle.net/2433/250313
Daigo Okada, Ryo Yamada (2020). Decomposition of a set of distributions in extended exponential family form for distinguishing multiple oligo-dimensional marker expression profiles of single-cell populations and visualizing their dynamics. PLOS ONE, 15(4):e0231250.
詳しい研究内容について
―低次元空間上でフローサイトメトリーの時系列動画も再現!―
概要
京都大学大学院医学研究科統計遺伝学分野 岡田大瑚 博士課程学生と山田亮 同教授は、複雑な確率分布に幾何的な座標を与える新規の統計手法である DEEF 法を開発し、細胞集団プロファイルの違いや変化を定量・可視化することに成功しました。生体内の細胞1つ1つのタンパク質や遺伝子の発現量はどれも同じではなく少しずつ違っているため、その細胞集団全体としての性質はこれらの細胞集団が作る分布として特徴づけることができます。このような分布は、細胞1つ1つに発現している遺伝子やタンパク質量を多数の細胞について測定する1細胞発現解析によって測定することができます。一方で、情報科学の分野では、確率分布同士の違いを幾何学的に研究する情報幾何学が発展してきました。本研究では、1細胞発現データのような複雑な分布に対して情報幾何的な座標を与え、ぞれぞれの座標が説明するパターンを抽出する新しい統計手法を開発し、細胞集団プロファイルの違いや変化を低次元空間上で定量・可視化することに成功しました。
この手法の面白い応用例としては、経時的に観測したフロサイトメトリーデータ注1)から、観測時刻と観察時刻の間の分布状態を推測し、動画を再構成することが挙げられます。
本研究成果は、2020 年 4 月 11 日に国際学術誌「PLOS ONE」のオンライン版に掲載されました。
1.背景
1細胞発現データは、細胞1つ1つに発現している遺伝子やタンパク質量を多数の細胞について測定する技術です。1細胞発現データから細胞サブセットを分類したり未知の細胞サブセットを発見するデータ解析手法は数多く開発されてきた一方で、複数の1細胞発現データを比較する手法は非常に限られていました。生体内の細胞1つ1つのタンパク質や遺伝子の発現量はばらつきがあり、その細胞集団全体としての性質はこれらのデータから得られる分布として特徴づけることができます。そこで本研究では、分布同士の違いを幾何学的に研究する情報幾何学を、細胞集団プロファイルの違いの解析に応用できることに着目しました。
2.研究手法・成果
正規分布や二項分布など多くの確率分布が指数型分布族という分布に属します。指数型分布族は、その幾何学的な性質が情報幾何学という分野でよく研究されています。一方で、生命科学で頻繁に登場する複雑な分布の中には、これに該当しないものもたくさんあります。本研究では、まず、任意の確率分布を指数型分布族様の表現を行なうために、指数型分布族の定義を拡張した拡大指数型分布族を新規に定義しました。次に、拡大指数型分布族の性質に基づいて、任意の分布セットの構成分布に対し、拡大指数型表現での座標を与える行列演算アルゴリズムを開発しました。実際にこのアルゴリズムを用いて、実際のデータを用いて細胞集団プロファイルのダイナミクスの描画、主要なパターンの抽出、タイムコースの補完ができることを示しました。(前ページ図、実例動画 URL:https://github.com/DaigoOkada/DEEF_press_gif/issues/1)
3.波及効果、今後の予定
DEEF法によって、細胞集団プロファイルに情報幾何的な座標が付与できます。これにより、豊富な統計・機械学習技術を 1 細胞発現データに適用できるようになりました。サイトメトリーデータを用いて疾患などに関連する細胞集団プロファイルの特徴を解明することにつながると考えています。一方で、今回の手法は数マーカー程度の比較的少ない数のマーカータンパク質/遺伝子のデータに対して適用可能であり、より多くのマーカー数のデータに適用することは難しいという課題があります。このような高次元データに対応できるように手法を拡張することが今後の課題です。
4.研究プロジェクトについて
本研究は、科研費助成事業(JP19J14816)、JST CREST「動く1細胞の「意思」を読み取るin vivo網羅的動態・発現解析法の開発」および JST CREST「離散構造統計学の創出と癌科学への展開」の支援を受けて京都大学で実施されました。
<用語解説>
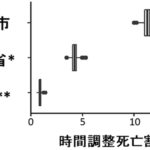
注1 フロサイトメトリーデータ:細胞1つ1つについて、いくつかの分子の発現量を計測データする実験によって得られるデータ。多くの場合、血液中の多数の(例えば 10 万個)白血球について測定するので、発現の様子を図で表すと雲がたなびいたような濃淡画像が得られる。
<論文タイトルと著者>
タイトル:Decomposition of a set of distributions in extended exponential family form for distinguishing multiple oligo-dimensional marker expression profiles of single-cell populations and visualizing their dynamics(分布セットを拡大指数型分布族表現に分解することによる、1 細胞発現プロファイルの識別とダイナミクスの可視化)
著 者:Daigo Okada and Ryo Yamada
掲 載 誌:PLOS ONE
U R L:https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0231250