2020-01-16 広島大学,科学技術振興機構
ポイント
- 蕁麻疹はよくある皮膚疾患で、さまざまな形や大きさの発疹(膨疹)が現れますが、それらがなぜ、どのようにしてその形で現れるか分かっていませんでした。
- 本研究では、反応拡散モデルと呼ばれる数学的な方程式を基に、膨疹形成の数理モデルを構築することに成功しました。
- 数理モデルによる分析から、臨床的に観察される膨疹には、従来考えられてきたヒスタミンの作用とそれに対する抑制性の作用の2つの機序が関与することが予測されます。
- 今後、数理モデルから予測される抑制系に関わる分子や機序が生物学的手法により分子レベルで同定され、蕁麻疹の病態理解が進み、膨疹の形態分析に基づく新たな病型分類や治療法の確立につながることが期待されます。
広島大学 大学院統合生命科学研究科 李 聖林 准教授、広島大学 大学院医系科学研究科 皮膚科学 秀 道広 教授、高萩 俊輔 助教、柳瀬 雄輝 助教は、蕁麻疹の定性的な臨床データと数理モデルを融合することにより、蕁麻疹でみられる発疹(膨疹)の多様な形を数理モデルで再現することに成功しました。
蕁麻疹では、その種類や患者さんにより、さまざまな形、大きさの膨疹が現れますが、これまでその多様な形態がどのようにして形成されるのかは分かっていませんでした。
本研究では、数学的手法である反応拡散モデルを用い、膨疹形成の数理モデルを構築することに成功しました。そのモデルからは、蕁麻疹の膨疹形成には従来から考えられてきたヒスタミンの作用のほか、それに対する抑制性の機序が関与することが予測されました。
今後、生物学的手法によりその抑制系の機序および分子が同定されることにより、蕁麻疹の病態理解が進み、ひいては膨疹の形態分析に基づく新たな病型分類あるいは治療法の確立につながる可能性があります。
本研究成果は、ロンドン時間の2020年1月15日午後7時(日本時間:2020年1月16日午前4時)「PLOS Computational Biology」オンライン版に掲載されます。
本成果は、以下の事業・研究領域・研究課題によって得られました。
戦略的創造研究推進事業 個人型研究(さきがけ)
研究領域:「社会的課題の解決に向けた数学と諸分野の協働」
(研究総括:國府 寛司 京都大学 大学院理学研究科 教授)
研究課題名:「動的変形空間による細胞機能決定機構の解明及びIn vitro実験への検証」
(研究者:李 聖林 広島大学 大学院統合生命科学研究科 准教授)
<背景>
蕁麻疹はよくある皮膚疾患で、皮膚の発赤を伴う腫れ(膨疹)が短時間のうちに現れたり消えたりすることを特徴とします。中には食物や薬剤が原因のこともありますが、多くは原因不明で虫刺症様、環状、花びら状、あるいは線状などの形をとり、大きさでは粟粒くらいの小さいものから手のひらサイズ、あるいはそれ以上に及ぶものまで多様な形を示します。それらはある程度まで蕁麻疹の病型あるいは個々の患者さんごとに関連する特徴がありますが、これまでどのようにしてそれらの形が形成されるかは分かっていませんでした。
<研究内容>
蕁麻疹で観察される膨疹は、蕁麻疹の病型によらず、その膨疹は皮膚マスト細胞から放出されたヒスタミンが血管に作用することで形成されることが知られています(図1)。しかし、それだけでは病型あるいは個々の患者ごとに固有の形や大きさの膨疹の形成機序を十分に説明することはできません。一方、数式を用いた反応拡散モデルは、すべての反応が一斉に起こるのではなく、どこか一部で起きた反応が次の反応を起こし、それが次々と拡散する仕組みが説明できます。本研究では、患部で観察された膨疹の形とその変化を反応拡散モデルを用いて解析し、蕁麻疹でみられる多様な形の膨疹を再現することに成功しました(図2)。また、そのモデルから、膨疹の形成には従来考えられてきたヒスタミンの作用(正の作用)とそれを打ち消す抑制性の作用(負の作用)が関与することが予測されました。
本研究は、JST 戦略的創造研究推進事業の研究課題の数理的成果の発展研究として、蕁麻疹の膨疹の幾何学的な形態パターンに着目し、膨疹形成の仕組みを数理モデルで解析、予測することを提案しています。
<今後の展開>
本研究から、蕁麻疹の多様な膨疹の形態形成には、皮膚マスト細胞から放出されるヒスタミンの作用とそれを抑制する作用の両方が寄与することが予測されました。今後、生物学的な実験手法によりその抑制系の機序と分子が同定されることにより、蕁麻疹の病態の理解を深め、形態解析による蕁麻疹の新しい病型分類や適切な治療の選択ができるようになることが期待されます。ひいては、蕁麻疹以外の特徴的な形の発疹が現れる皮膚疾患についても、数理モデルによる数学的解析を通じて病態の理解や治療の有効性を予測する新しい分野が開ける可能性もあります。
<参考図>
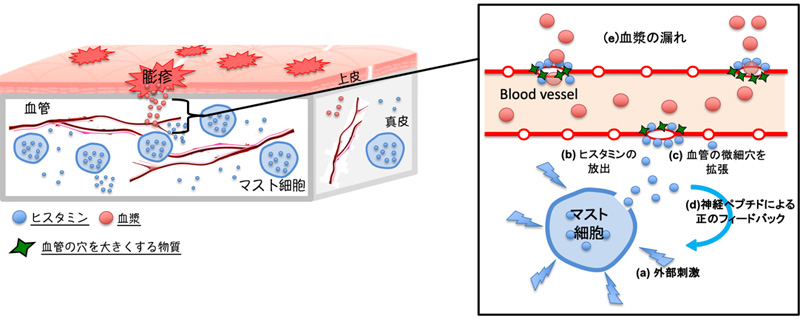 図1 蕁麻疹における膨疹の形成機序
図1 蕁麻疹における膨疹の形成機序
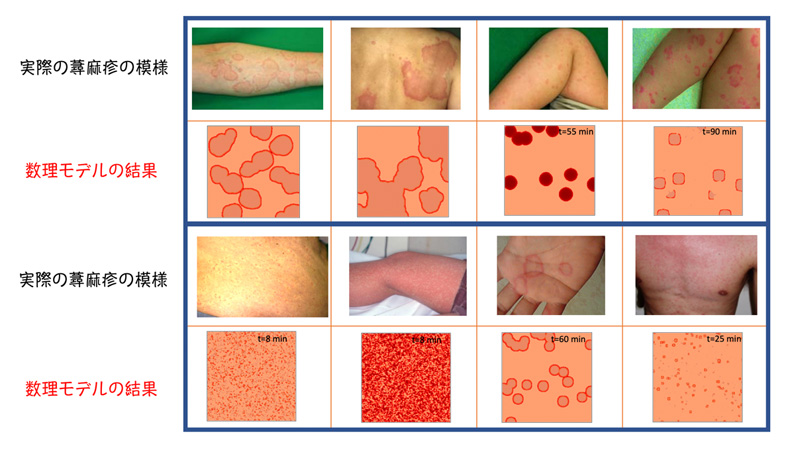
図2 蕁麻疹でみられる多様な幾何学的形態と数理モデルにより再現された膨疹の形態
<論文タイトル>
- “A Single Reaction-Diffusion Equation for the Multifarious Eruptions of Urticaria”
- 著者:李 聖林、柳瀬 雄輝、高萩 俊輔、秀 道広
- DOI:10.1371/journal.pcbi.1007590
<お問い合わせ先>
<研究に関すること>
李 聖林(リ セイリン)
広島大学 大学院統合生命科学研究科 数理生命科学プログラム 准教授
秀 道広(ヒデ ミチヒロ)
広島大学 大学院医系科学研究科 皮膚科学 教授
<JST事業に関すること>
舘澤 博子(タテサワ ヒロコ)
科学技術振興機構 戦略研究推進部 ICTグループ
<報道担当>
広島大学 広報グループ
科学技術振興機構 広報課