2019-10-02 京都大学,国立情報学研究所,科学技術振興機構
ポイント
- 神経回路の構造(シナプス結合)を分析することは脳の情報処理メカニズムを理解するうえで重要だが、周囲のニューロン(神経細胞)や外部信号の影響があり、高精度な推定は従来できなかった。
- 相互相関解析と一般化線形モデルを融合させた解析法GLMCCを開発。外部の影響を消し去り、ニューロン間のシナプス結合を高精度に把握することに成功した。
- この解析法によって各脳領野における情報の流れと情報処理の様式が明らかにされていくことが期待される。
京都大学 大学院理学研究科 篠本 滋 准教授と国立情報学研究所 小林 亮太 助教は、理化学研究所、立命館大学、大阪市立大学、ドイツ・ユーリヒ研究所、米国立衛生研究所の研究者と共同で、神経活動データからその背後にある脳神経回路を高精度で推定する解析法を開発しました。
計測技術の驚異的進展により、神経科学においては多数のニューロンの信号を長時間にわたって計測できるようになりました。神経活動にはニューロン間のつながりが影響しますから、計測された神経信号を分析すれば結合を推定することができるはずです。この考え方は50年以上前から提案されていましたが、信号にはシナプス結合の影響だけではなく、周囲のニューロンの影響や外部信号の影響も加わっていて現象が複雑で、これまでには信頼性の高い推定は得られていませんでした。
本研究では機械学習理論で発展した一般化線形モデルを用いて外部の影響を消し去り、ニューロン間のシナプス結合(脳の回路図)を把握することに成功しました。大規模シミュレーションデータや実験データに適用した結果、新手法が従来手法に比べてはるかに高い推定精度を有することを確認しました。
最新の計測技術を駆使してさまざまな脳領野から多くの神経信号が計測され始めていますので、この解析法によって各脳領野における情報の流れと情報処理の様式が明らかにされていくと期待されます。解析プログラムは研究者が自由に使えるように公開しており、Webアプリケーションも提供しています。
本成果は、2019年10月2日(日本時間)に国際学術誌「Nature Communications」にオンライン掲載されます。
本研究は京都大学 篠本 滋、国立情報学研究所 小林 亮太(JST 戦略的創造研究推進事業 ACT-I研究領域「情報と未来」の研究課題「時系列データの自動解析技術の実現」研究者)に加えて、理化学研究所 栗田 修平、立命館大学 北野 勝則、大阪市立大学 水関 健二、ドイツ・ユーリヒ研究所 Anno Kurth、Markus Diesmann、米国立衛生研究所 Barry J Richmondが加わった共同研究です。
脳の情報処理メカニズムを理解するためには、神経回路の構造を知る必要がありますが、これまでその大規模な分析はなされていませんでした。近年の信号計測技術の進展によって数多くのニューロンが発生するスパイク信号注1)を長時間にわたって記録できるようになり、それらの信号を解析すれば多数のニューロン間のつながり(シナプス結合)を推定できることが期待されています。これは、ニューロンAからニューロンBに正の(興奮性)シナプス結合があれば、Aが活動した後にはBが活動する頻度が上がり、負の(抑制性)シナプス結合があれば活動頻度が下がりますので、信号時系列の相関を調べることによって神経結合を推定することができるはずです。こういう考え方そのものは50年以上前から提案されていましたが、神経信号にはニューロン間の結合による直接の影響のみならず、その他のニューロンを介した間接的な影響や外部信号の影響も加わっていて現象が複雑であり、これまでは十分信頼性のおける推定をすることができていませんでした。
本研究では並列信号時系列の相互相関(Cross Correlation,CC)からニューロン間の結合(脳の回路図)を高精度で推定する解析法を構築しました(図1)。今回、機械学習の基盤技術として確立してきた一般化線形モデル注2)(Generalized Linear Model,GLM)を利用して外部信号の影響を消し、ニューロン間の神経結合を抽出します(図2)。相互相関にある、ゆっくりと変動する外部信号成分と神経結合成分を分離することに新たに着目することにより、スパイク信号から神経結合を自動的に抽出することに成功しました。「GLMCC」(Generalized Linear Model for Cross Correlation)と名付けられたこの解析法は、神経結合の強さをシナプス膜電位の単位で推定することができます。また求めたい膜電位レベルに応じて必要な計測時間の見積もりを与える公式注3)も導出しました。
次に、結合推定の精度を評価するために1,000個のモデルニューロン(神経細胞モデル)からなる神経回路のシミュレーションを行いました。シミュレーションデータを用いて検証した結果、新手法は従来手法に比べて、はるかに高い推定精度(精度:97パーセント、MCC:0.7)を有することを確認しました注4)。新手法によって、既存手法では難しかった抑制性結合の正確な推定が可能になりました。さらに、脳の局所回路に近い10,000個のモデルニューロンからなる大規模神経回路のシミュレーションを行い、新手法の有効性を確認しました。
最後にラットから計測された実験データに適用し、海馬の神経細胞間の神経結合を推定しました。神経細胞には、興奮性の結合だけを出力する興奮性細胞と抑制性の結合だけを出力する抑制性細胞があります。スパイク波形や神経活動の様子などから専門家が判定した興奮性・抑制性細胞と推定された興奮性・抑制性細胞は一致していることを確認しました。また、神経細胞間の結合確率はこれまでスライス実験で確認されたものと整合している(結合確率はおよそ3パーセント)ことを確認しました。
本研究で構築された解析法により、神経信号時系列から脳の神経回路についての推定が高精度で得られます。また得られた公式によって、実験家は推定に必要な計測時間を前もって見積もることができます。今後は最新の計測技術によってさまざまな脳領野から数多くの神経ビッグデータが得られてくるでしょうから、この解析法によって脳内の異なる機能領域における情報処理や情報の流れの違いを明らかにすることができると期待されます。解析プログラムは自由に使えるように公開しており、研究者が自由に使えるWebアプリケーションも提供しています(http://www.ton.scphys.kyoto-u.ac.jp/~shino/GLMCC/)。
図1
並列計測される神経スパイク信号に本研究の解析プログラム「GLMCC」(Generalized Linear Model for Cross Correlation)を適用することにより脳の回路図(ニューロン間のシナプス結合)を得ることができます。
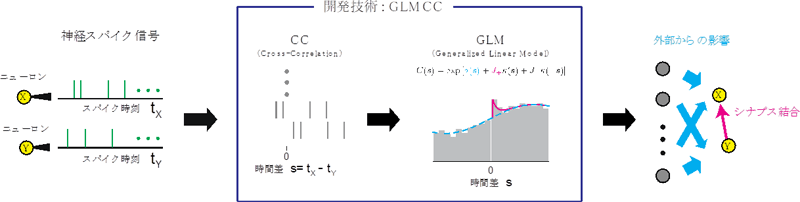
図2
開発技術「GLMCC」の模式図。GLMCCでは、2つのニューロンのスパイク時系列の相互相関(CC)を計算します。次に、一般化線形モデル(GLM)を相互相関に適用することにより、外部からの影響(シアン:a(s))を取り除きながら、ニューロン間のシナプス結合の強さ(マゼンタ:J+)を抽出します。
- 注1)スパイク信号
- 神経細胞は、強い刺激を受けるとスパイク(活動電位)と呼ばれるパルスを生成します。ニューロンはスパイクの波形ではなく、スパイクを生成した時刻によって情報を表現していると考えられています。そのため、スパイク信号とは神経細胞がスパイクを生成した時刻のこととなります。図1のイラスト中の緑の縦線は5個の神経細胞のスパイク信号を表しています。
- 注2)一般化線形モデル
- 統計解析で広く使われる線形モデルは、(1)従属変数Yと独立変数Xの間には線形関係Y=aX+bが成り立ち、(2)誤差分布が正規分布である、という数理モデルです。一方、一般化線形モデル(Nelder and Wedderburn 1972)は、(1)従属変数をリンク関数gで変換したg(Y)と独立変数Xの間には線形関係、g(Y)=aX+b、が成り立ち、(2)誤差分布が指数型分布である、という数理モデルです。これら2点の拡張により、一般化線形モデルは実世界のさまざまなデータを表現できます。また、一般化線形モデルは機械学習や統計学で広く用いられています。例えば、機械学習の代表的な手法であるロジスティック回帰は一般化線形モデルになります。
- 注3)求めたい膜電位レベルに応じて必要な計測時間の見積もりを与える公式
- 神経結合の推定に必要となる計測時間Tは以下のように書けることを示しました:T∝(λXλYw2)-1。ただし、λX(Y)は細胞X(Y)の活動度(発火率)、wはシナプス膜電位になります。
- 注4)新手法は従来手法に比べて、はるかに高い推定精度(精度:97パーセント、MCC:0.7)を有することを確認しました。
- これまで神経結合推定に用いられてきた代表的な手法として、相互相関法(Aertsen and Gerstein 1985)とJittering法(Amarasingham et al.,2012)があります。既存手法の推定精度は、相互相関法(精度:77パーセント、MCC:0.4)、Jittering法(精度:93パーセント、MCC:0.2)でした。精度(Accuracy)、MCC(Matthews correlation coefficient)は機械学習の2値分類問題で使われる評価指標です。精度は正しい神経結合を検出できた割合を表し、数値が大きいほど性能が高いことを示します。精度は全てを正しく推定できた場合には100パーセント、全てが失敗した場合には0パーセントになります。また、MCCは出現頻度が大きく異なる2値分類問題に対して有効な指標であり、相関係数を2値変数に拡張したものです。MCCは-1から1までの値を取り、数値が大きいほど性能が高いことを示します。MCCは全てを正しく推定できた場合には1、ランダムに推定された場合には0を取ります。
- “Reconstructing Neuronal Circuitry from Parallel Spike Trains”
(並列計測される神経スパイク信号から神経回路を再構成する) - 著者名:Ryota Kobayashi, Shuhei Kurita, Anno Kurth, Katsunori Kitano, Kenji Mizuseki, Markus Diesmann, Barry J. Richmond, and Shigeru Shinomoto
- DOI:10.1038/s41467-019-12225-2
篠本 滋(シノモト シゲル)
京都大学 大学院理学研究科 物理学宇宙物理学専攻 准教授
小林 亮太(コバヤシ リョウタ)
国立情報学研究所 情報学プリンシプル研究系 助教
舘澤 博子(タテサワ ヒロコ)
科学技術振興機構 戦略研究推進部
京都大学 総務部 広報課 国際広報室
情報・システム研究機構 国立情報学研究所 総務部 企画課 広報チーム
科学技術振興機構 広報課